Community Detection in Degree-Corrected Block Models
Paper and Code
Jul 24, 2016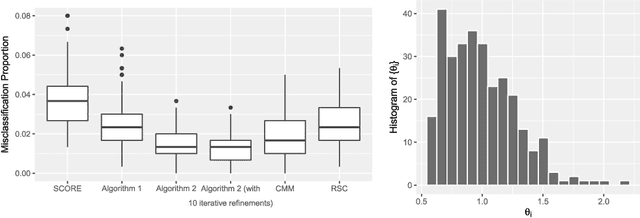

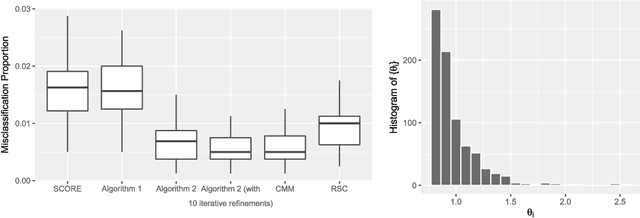
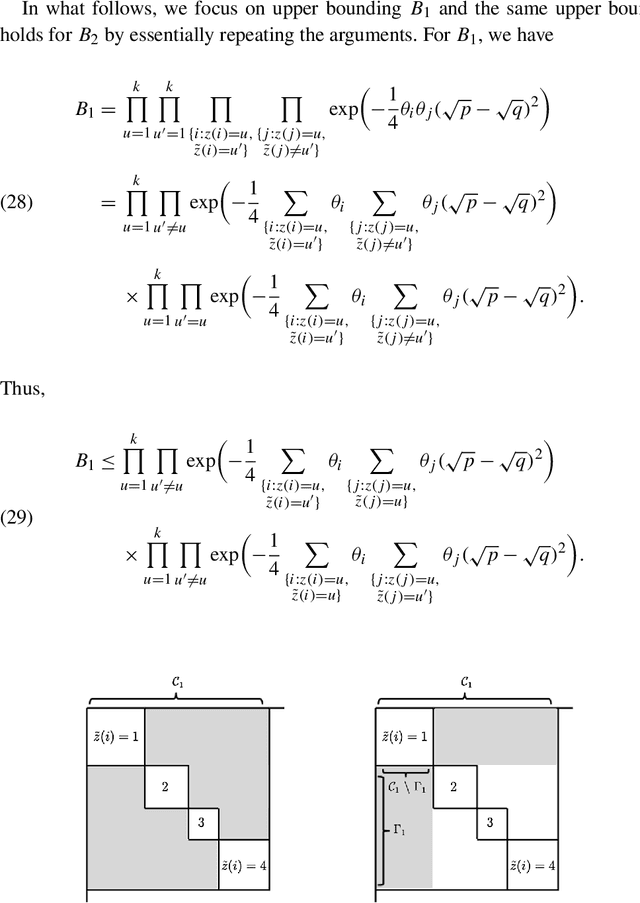
Community detection is a central problem of network data analysis. Given a network, the goal of community detection is to partition the network nodes into a small number of clusters, which could often help reveal interesting structures. The present paper studies community detection in Degree-Corrected Block Models (DCBMs). We first derive asymptotic minimax risks of the problem for a misclassification proportion loss under appropriate conditions. The minimax risks are shown to depend on degree-correction parameters, community sizes, and average within and between community connectivities in an intuitive and interpretable way. In addition, we propose a polynomial time algorithm to adaptively perform consistent and even asymptotically optimal community detection in DCBMs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge