Communication efficient privacy-preserving distributed optimization using adaptive differential quantization
Paper and Code
May 30, 2021
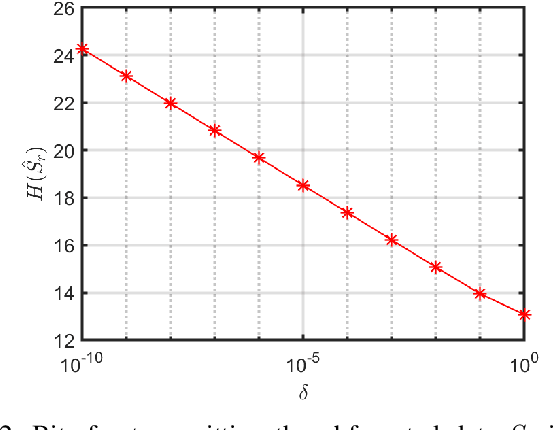
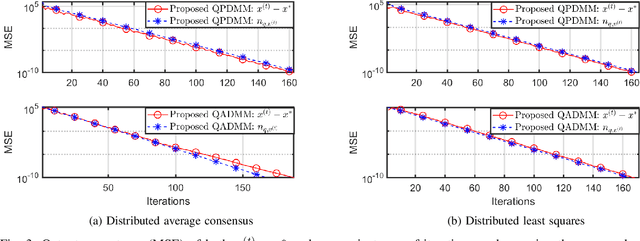
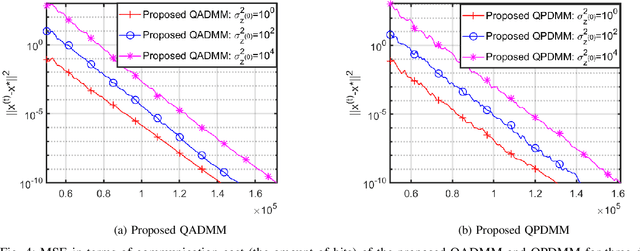
Privacy issues and communication cost are both major concerns in distributed optimization. There is often a trade-off between them because the encryption methods required for privacy-preservation often incur expensive communication bandwidth. To address this issue, we, in this paper, propose a quantization-based approach to achieve both communication efficient and privacy-preserving solutions in the context of distributed optimization. By deploying an adaptive differential quantization scheme, we allow each node in the network to achieve its optimum solution with a low communication cost while keeping its private data unrevealed. Additionally, the proposed approach is general and can be applied in various distributed optimization methods, such as the primal-dual method of multipliers (PDMM) and the alternating direction method of multipliers (ADMM). Moveover, we consider two widely used adversary models: passive and eavesdropping. Finally, we investigate the properties of the proposed approach using different applications and demonstrate its superior performance in terms of several parameters including accuracy, privacy, and communication cost.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge