Common Information Components Analysis
Paper and Code
Feb 28, 2020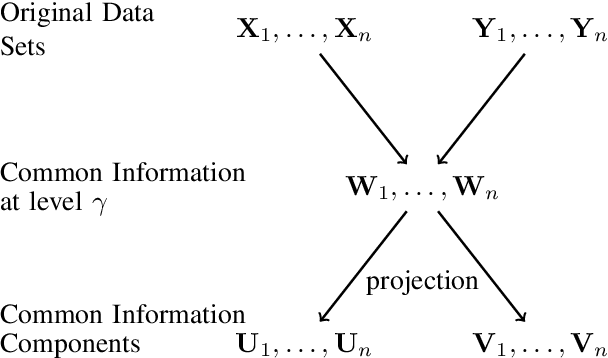
We give an information-theoretic interpretation of Canonical Correlation Analysis (CCA) via (relaxed) Wyner's common information. CCA permits to extract from two high-dimensional data sets low-dimensional descriptions (features) that capture the commonalities between the data sets, using a framework of correlations and linear transforms. Our interpretation first extracts the common information up to a pre-selected resolution level, and then projects this back onto each of the data sets. In the case of Gaussian statistics, this procedure precisely reduces to CCA, where the resolution level specifies the number of CCA components that are extracted. This also suggests a novel algorithm, Common Information Components Analysis (CICA), with several desirable features, including a natural extension to beyond just two data sets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge