Combining Geometric and Information-Theoretic Approaches for Multi-Robot Exploration
Paper and Code
Apr 15, 2020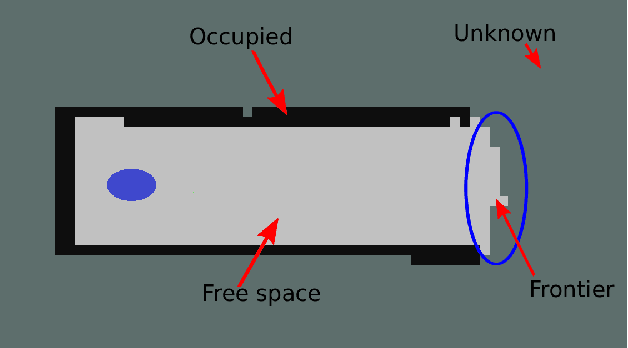
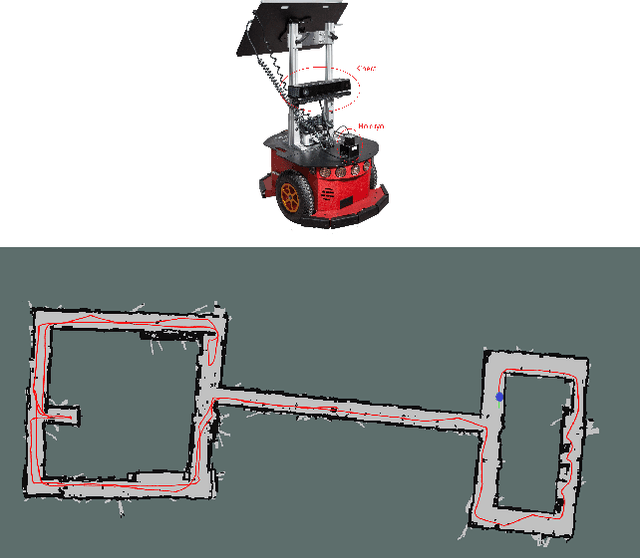
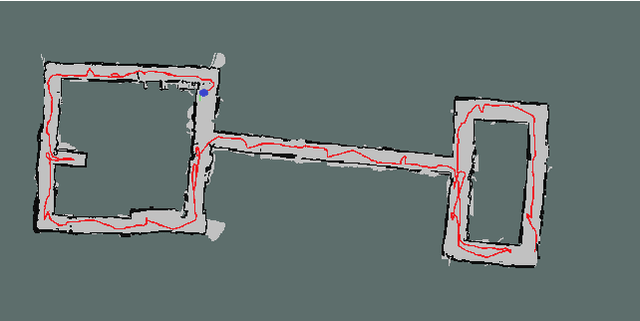
We present an algorithm to explore an orthogonal polygon using a team of $p$ robots. This algorithm combines ideas from information-theoretic exploration algorithms and computational geometry based exploration algorithms. We show that the exploration time of our algorithm is competitive (as a function of $p$) with respect to the offline optimal exploration algorithm. The algorithm is based on a single-robot polygon exploration algorithm, a tree exploration algorithm for higher level planning and a submodular orienteering algorithm for lower level planning. We discuss how this strategy can be adapted to real-world settings to deal with noisy sensors. In addition to theoretical analysis, we investigate the performance of our algorithm through simulations for multiple robots and experiments with a single robot.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge