Combining Experimental and Observational Data for Identification of Long-Term Causal Effects
Paper and Code
Jan 26, 2022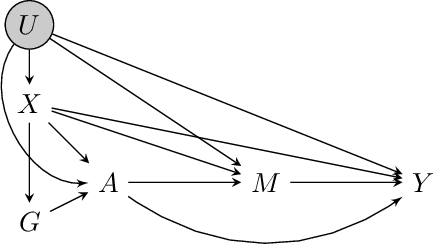
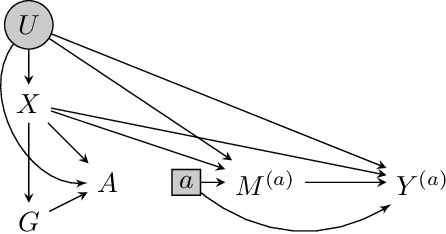
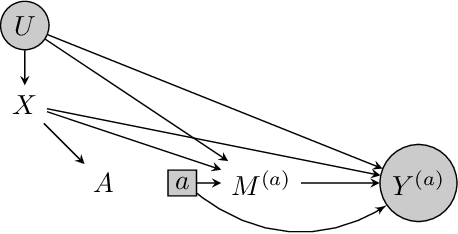
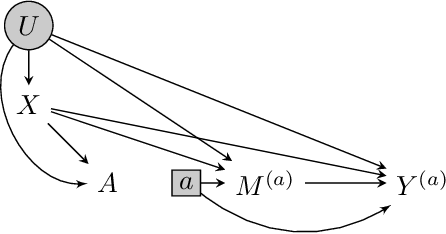
We consider the task of estimating the causal effect of a treatment variable on a long-term outcome variable using data from an observational domain and an experimental domain. The observational data is assumed to be confounded and hence without further assumptions, this dataset alone cannot be used for causal inference. Also, only a short-term version of the primary outcome variable of interest is observed in the experimental data, and hence, this dataset alone cannot be used for causal inference either. In a recent work, Athey et al. (2020) proposed a method for systematically combining such data for identifying the downstream causal effect in view. Their approach is based on the assumptions of internal and external validity of the experimental data, and an extra novel assumption called latent unconfoundedness. In this paper, we first review their proposed approach and discuss the latent unconfoundedness assumption. Then we propose two alternative approaches for data fusion for the purpose of estimating average treatment effect as well as the effect of treatment on the treated. Our first proposed approach is based on assuming equi-confounding bias for the short-term and long-term outcomes. Our second proposed approach is based on the proximal causal inference framework, in which we assume the existence of an extra variable in the system which is a proxy of the latent confounder of the treatment-outcome relation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge