Combination of LMS Adaptive Filters with Coefficients Feedback
Paper and Code
Nov 19, 2017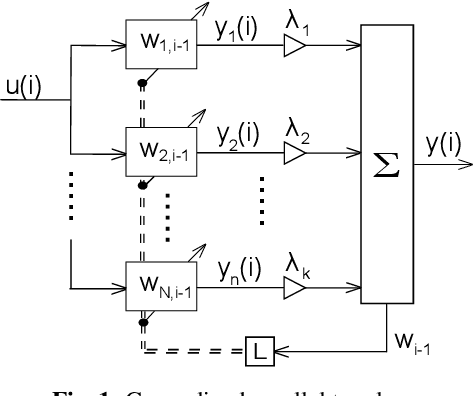
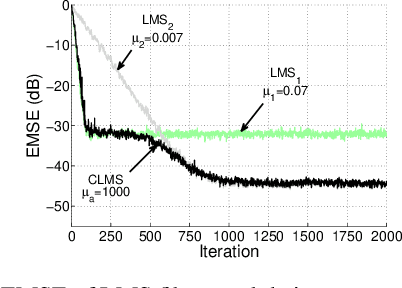
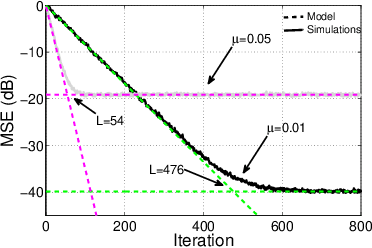
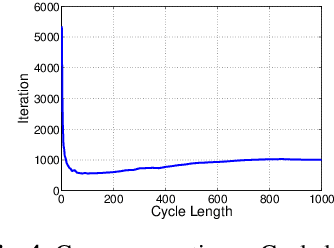
Parallel combinations of adaptive filters have been effectively used to improve the performance of adaptive algorithms and address well-known trade-offs, such as convergence rate vs. steady-state error. Nevertheless, typical combinations suffer from a convergence stagnation issue due to the fact that the component filters run independently. Solutions to this issue usually involve conditional transfers of coefficients between filters, which although effective, are hard to generalize to combinations with more filters or when there is no clearly faster adaptive filter. In this work, a more natural solution is proposed by cyclically feeding back the combined coefficient vector to all component filters. Besides coping with convergence stagnation, this new topology improves tracking and supervisor stability, and bridges an important conceptual gap between combinations of adaptive filters and variable step size schemes. We analyze the steady-state, tracking, and transient performance of this topology for LMS component filters and supervisors with generic activation functions. Numerical examples are used to illustrate how coefficients feedback can improve the performance of parallel combinations at a small computational overhead.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge