Columnwise Element Selection for Computationally Efficient Nonnegative Coupled Matrix Tensor Factorization
Paper and Code
Mar 07, 2020
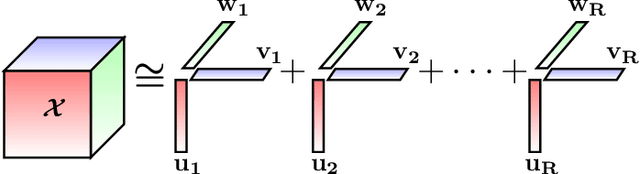
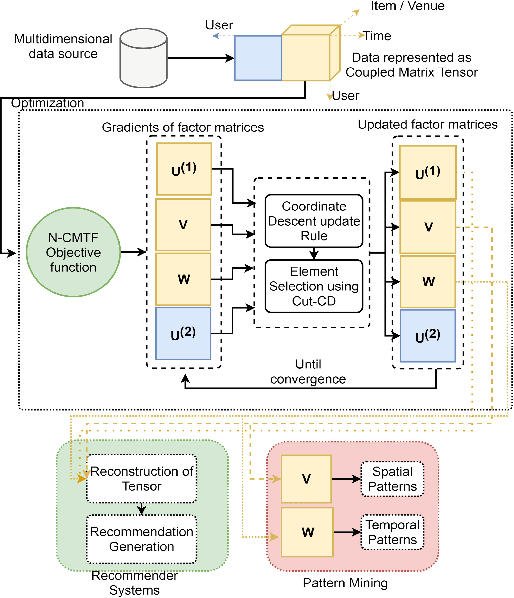
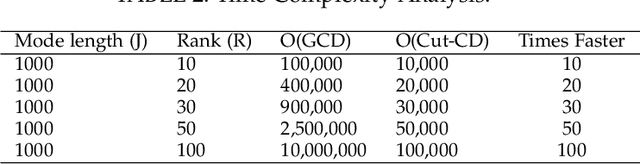
Coupled Matrix Tensor Factorization (CMTF) facilitates the integration and analysis of multiple data sources and helps discover meaningful information. Nonnegative CMTF (N-CMTF) has been employed in many applications for identifying latent patterns, prediction, and recommendation. However, due to the added complexity with coupling between tensor and matrix data, existing N-CMTF algorithms exhibit poor computation efficiency. In this paper, a computationally efficient N-CMTF factorization algorithm is presented based on the column-wise element selection, preventing frequent gradient updates. Theoretical and empirical analyses show that the proposed N-CMTF factorization algorithm is not only more accurate but also more computationally efficient than existing algorithms in approximating the tensor as well as in identifying the underlying nature of factors.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge