Collaborative High Accuracy Localization in Mobile Multipath Environments
Paper and Code
Nov 08, 2012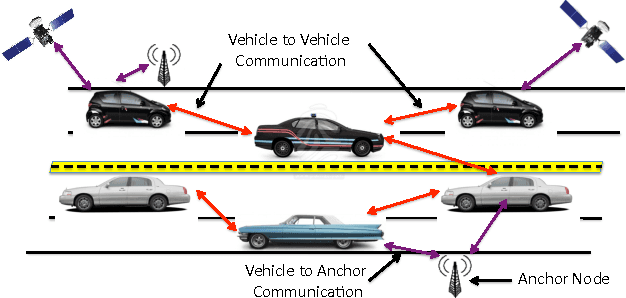
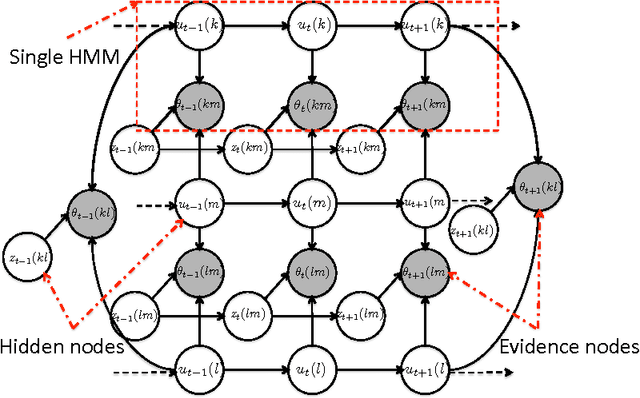
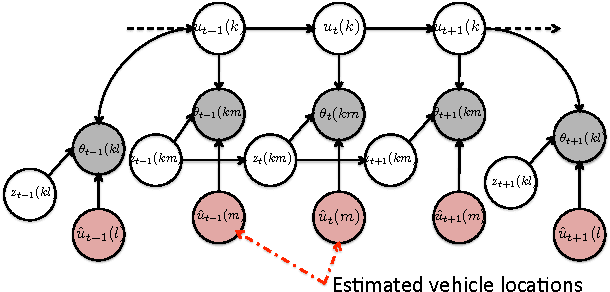
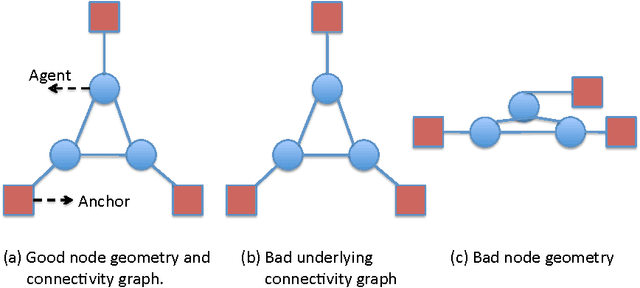
We study the problem of high accuracy localization of mobile nodes in a multipath-rich environment where sub-meter accuracies are required. We employ a peer-to-peer framework where the vehicles/nodes can get pairwise multipath-degraded ranging estimates in local neighborhoods together with a fixed number of anchor nodes. The challenge is to overcome the multipath-barrier with redundancy in order to provide the desired accuracies especially under severe multipath conditions when the fraction of received signals corrupted by multipath is dominating. We invoke a analytical graphical model framework based on particle filtering and reveal its high accuracy localization promise through simulations. We also address design questions such as "How many anchors and what fraction of line-of-sight (LOS) measurements are needed to achieve a specified target accuracy?", by analytically characterizing the performance improvement in localization accuracy as a function of the number of nodes in the network and the fraction of LOS measurements. In particular, for a static node placement, we show that the Cramer-Rao Lower Bound (CRLB), a fundamental lower bound on the localization accuracy, can be expressed as a product of two factors - a scalar function that depends only on the parameters of the noise distribution and a matrix that depends only on the geometry of node locations and the underlying connectivity graph. Further, a simplified expression is obtained for the CRLB that helps deduce the scaling behavior of the estimation error as a function of the number of agents and anchors in the network. The bound suggests that even a small fraction of LOS measurements can provide significant improvements. Conversely, a small fraction of NLOS measurements can significantly degrade the performance. The analysis is extended to the mobile setting and the performance is compared with the derived CRLB.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge