CobBO: Coordinate Backoff Bayesian Optimization
Paper and Code
Feb 16, 2021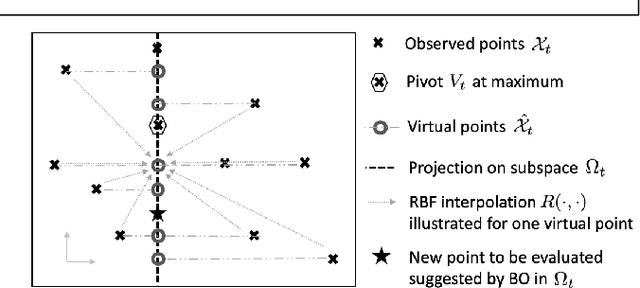

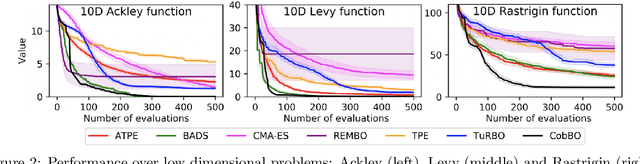

Bayesian optimization is a popular method for optimizing expensive black-box functions. The objective functions of hard real world problems are oftentimes characterized by a fluctuated landscape of many local optima. Bayesian optimization risks in over-exploiting such traps, remaining with insufficient query budget for exploring the global landscape. We introduce Coordinate Backoff Bayesian Optimization (CobBO) to alleviate those challenges. CobBO captures a smooth approximation of the global landscape by interpolating the values of queried points projected to randomly selected promising subspaces. Thus also a smaller query budget is required for the Gaussian process regressions applied over the lower dimensional subspaces. This approach can be viewed as a variant of coordinate ascent, tailored for Bayesian optimization, using a stopping rule for backing off from a certain subspace and switching to another coordinate subset. Extensive evaluations show that CobBO finds solutions comparable to or better than other state-of-the-art methods for dimensions ranging from tens to hundreds, while reducing the trial complexity.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge