CNNs are Globally Optimal Given Multi-Layer Support
Paper and Code
Dec 14, 2017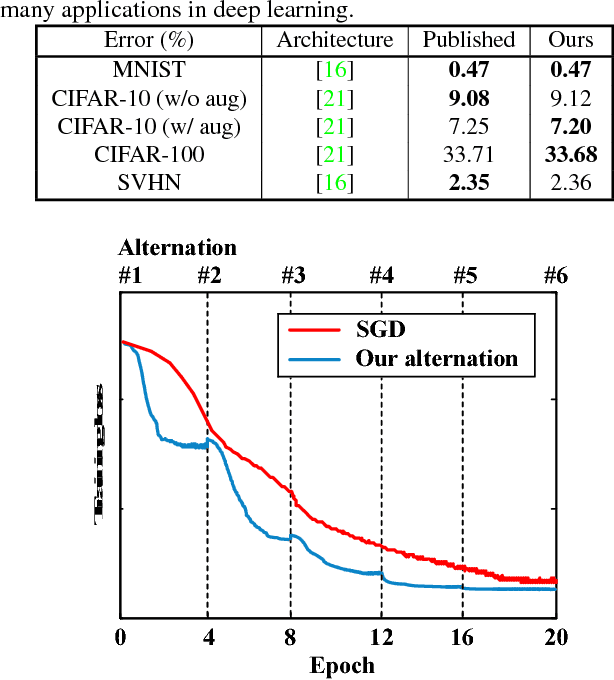
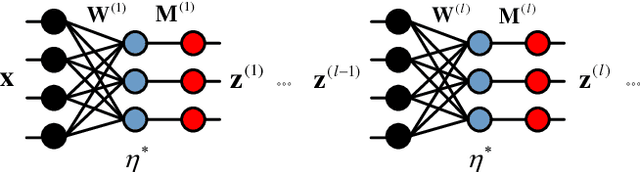
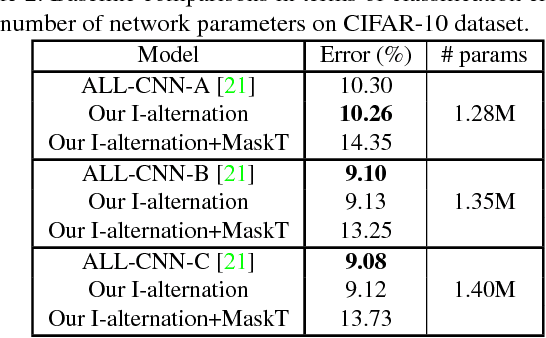
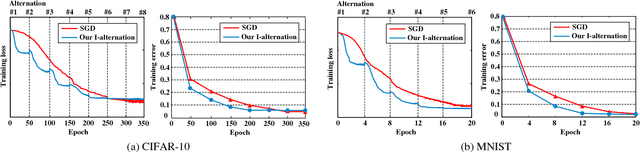
Stochastic Gradient Descent (SGD) is the central workhorse for training modern CNNs. Although giving impressive empirical performance it can be slow to converge. In this paper we explore a novel strategy for training a CNN using an alternation strategy that offers substantial speedups during training. We make the following contributions: (i) replace the ReLU non-linearity within a CNN with positive hard-thresholding, (ii) reinterpret this non-linearity as a binary state vector making the entire CNN linear if the multi-layer support is known, and (iii) demonstrate that under certain conditions a global optima to the CNN can be found through local descent. We then employ a novel alternation strategy (between weights and support) for CNN training that leads to substantially faster convergence rates, nice theoretical properties, and achieving state of the art results across large scale datasets (e.g. ImageNet) as well as other standard benchmarks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge