Clutter Edges Detection Algorithms for Structured Clutter Covariance Matrices
Paper and Code
Feb 03, 2022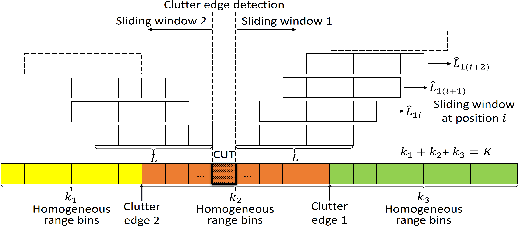
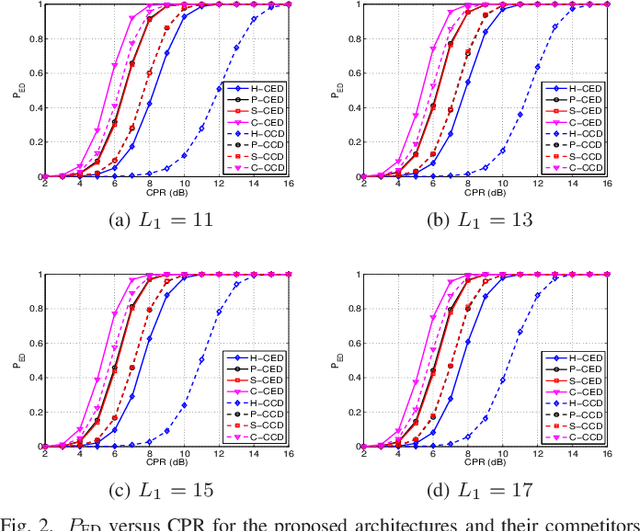
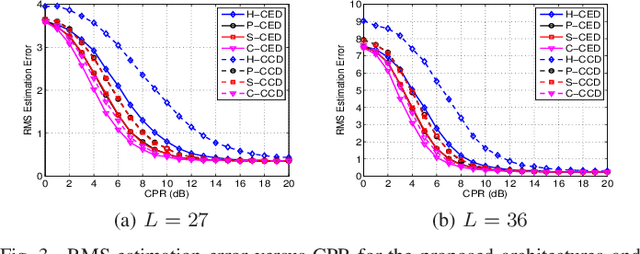
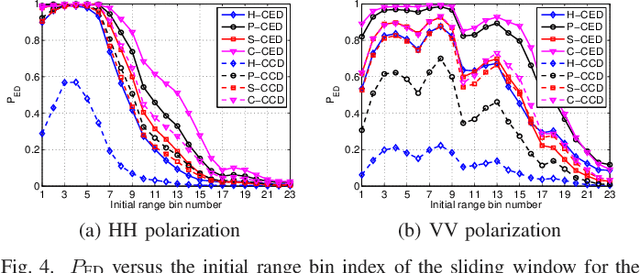
This letter deals with the problem of clutter edge detection and localization in training data. To this end, the problem is formulated as a binary hypothesis test assuming that the ranks of the clutter covariance matrix are known, and adaptive architectures are designed based on the generalized likelihood ratio test to decide whether the training data within a sliding window contains a homogeneous set or two heterogeneous subsets. In the design stage, we utilize four different covariance matrix structures (i.e., Hermitian, persymmetric, symmetric, and centrosymmetric) to exploit the a priori information. Then, for the case of unknown ranks, the architectures are extended by devising a preliminary estimation stage resorting to the model order selection rules. Numerical examples based on both synthetic and real data highlight that the proposed solutions possess superior detection and localization performance with respect to the competitors that do not use any a priori information.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge