Clustering with Confidence: Finding Clusters with Statistical Guarantees
Paper and Code
Dec 30, 2016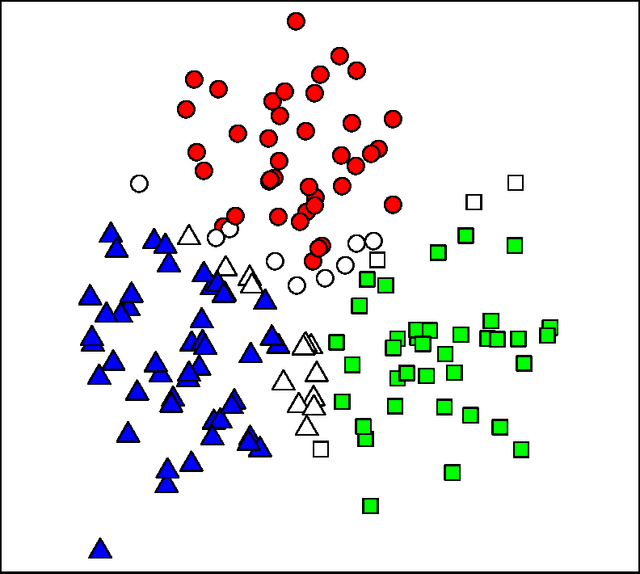
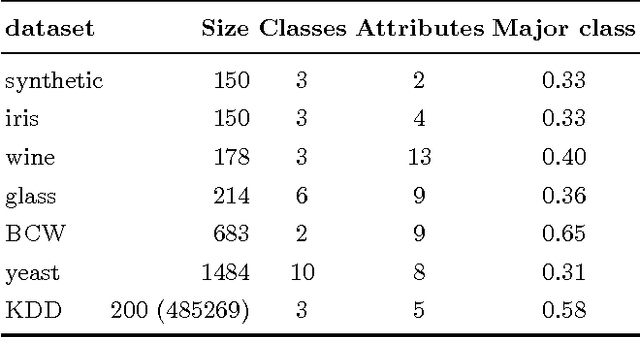

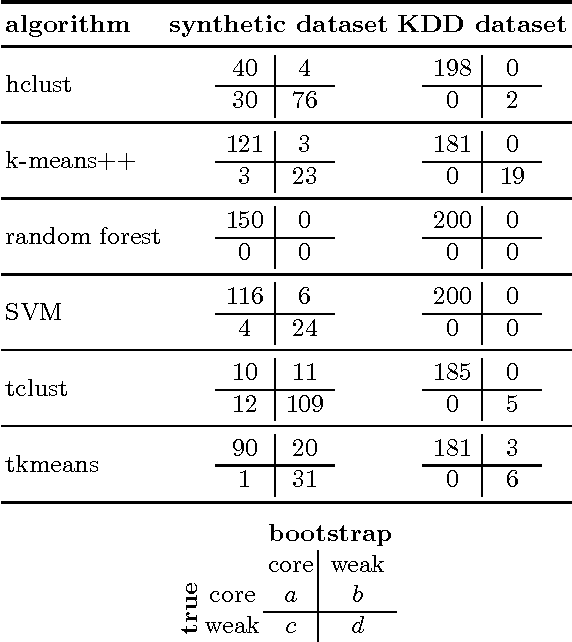
Clustering is a widely used unsupervised learning method for finding structure in the data. However, the resulting clusters are typically presented without any guarantees on their robustness; slightly changing the used data sample or re-running a clustering algorithm involving some stochastic component may lead to completely different clusters. There is, hence, a need for techniques that can quantify the instability of the generated clusters. In this study, we propose a technique for quantifying the instability of a clustering solution and for finding robust clusters, termed core clusters, which correspond to clusters where the co-occurrence probability of each data item within a cluster is at least $1 - \alpha$. We demonstrate how solving the core clustering problem is linked to finding the largest maximal cliques in a graph. We show that the method can be used with both clustering and classification algorithms. The proposed method is tested on both simulated and real datasets. The results show that the obtained clusters indeed meet the guarantees on robustness.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge