CLOSURE: Fast Quantification of Pose Uncertainty Sets
Paper and Code
Mar 15, 2024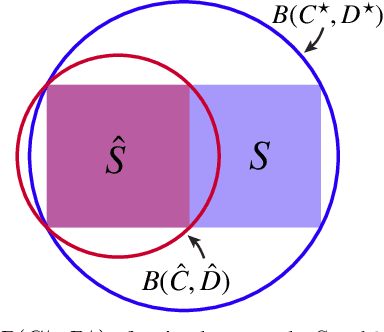
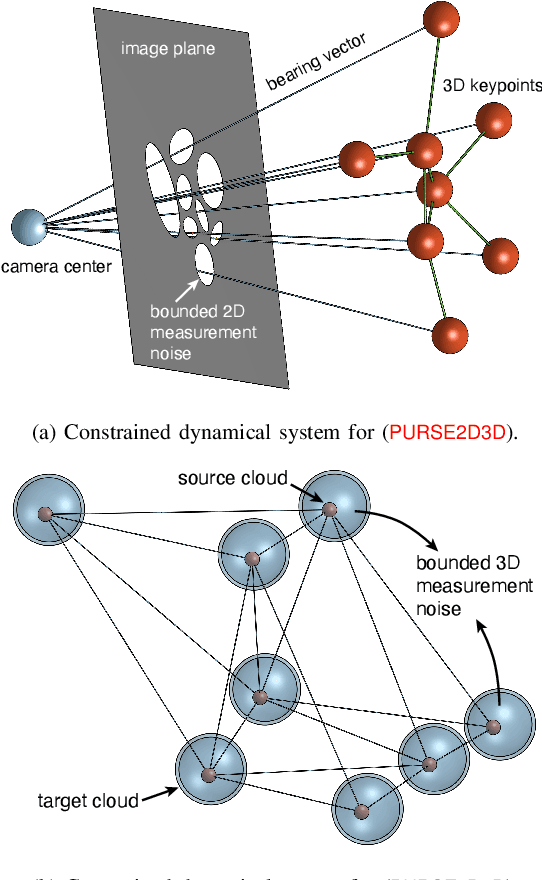
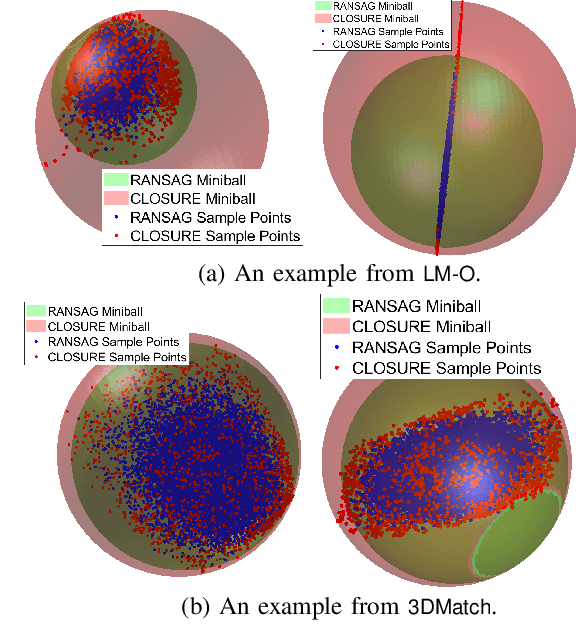
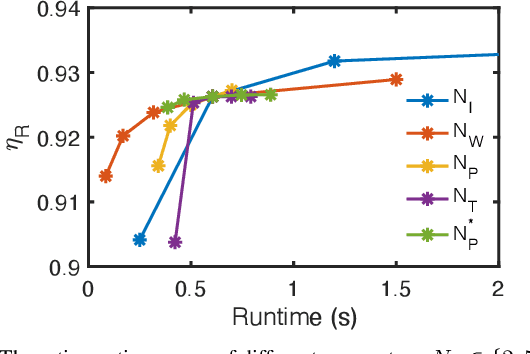
We investigate uncertainty quantification of 6D pose estimation from keypoint measurements. Assuming unknown-but-bounded measurement noises, a pose uncertainty set (PURSE) is a subset of SE(3) that contains all possible 6D poses compatible with the measurements. Despite being simple to formulate and its ability to embed uncertainty, the PURSE is difficult to manipulate and interpret due to the many abstract nonconvex polynomial constraints. An appealing simplification of PURSE is to find its minimum enclosing geodesic ball (MEGB), i.e., a point pose estimation with minimum worst-case error bound. We contribute (i) a dynamical system perspective, and (ii) a fast algorithm to inner approximate the MEGB. Particularly, we show the PURSE corresponds to the feasible set of a constrained dynamical system, and this perspective allows us to design an algorithm to densely sample the boundary of the PURSE through strategic random walks. We then use the miniball algorithm to compute the MEGB of PURSE samples, leading to an inner approximation. Our algorithm is named CLOSURE (enClosing baLl frOm purSe boUndaRy samplEs) and it enables computing a certificate of approximation tightness by calculating the relative size ratio between the inner approximation and the outer approximation. Running on a single RTX 3090 GPU, CLOSURE achieves the relative ratio of 92.8% on the LM-O object pose estimation dataset and 91.4% on the 3DMatch point cloud registration dataset with the average runtime less than 0.2 second. Obtaining comparable worst-case error bound but 398x and 833x faster than the outer approximation GRCC, CLOSURE enables uncertainty quantification of 6D pose estimation to be implemented in real-time robot perception applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge