Closed-Form Minkowski Sums of Convex Bodies with Smooth Positively Curved Boundaries

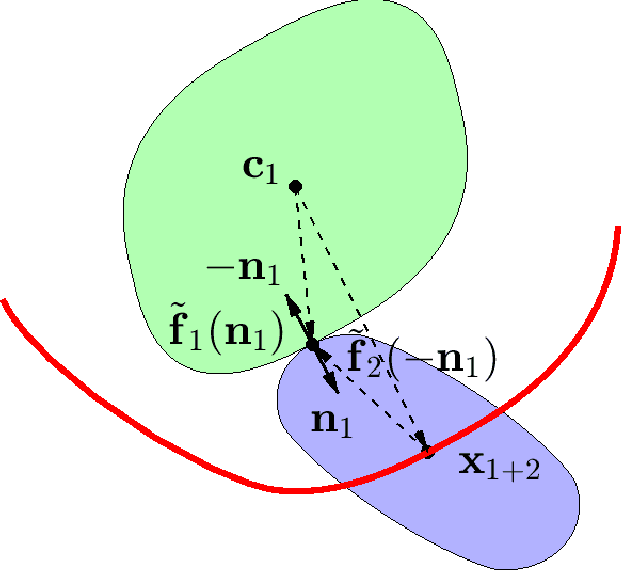
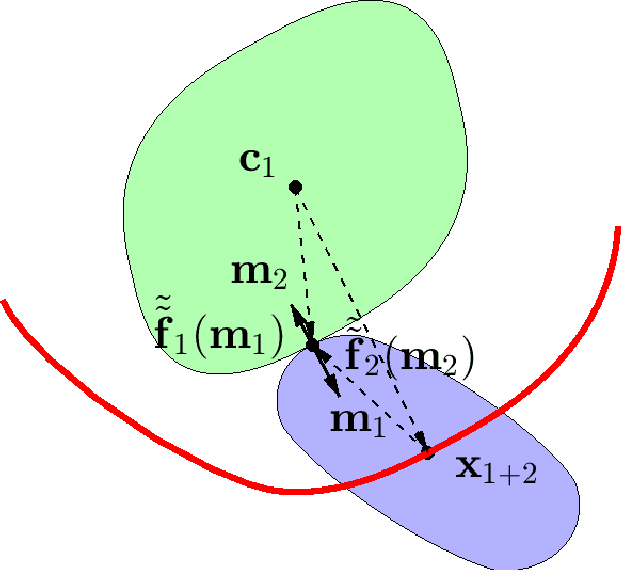
This paper proposes a closed-form parametric formula of the Minkowski sum boundary for broad classes of convex bodies in d-dimensional Euclidean space. With positive sectional curvatures at every point, the boundary that encloses each body can be characterized by the surface gradient. The first theorem directly parameterizes the Minkowski sums using the unit normal vector at each body surface. Although simple to express mathematically, such a parameterization is not always practical to obtain computationally. Therefore, the second theorem derives a more useful parametric closed-form expression using the gradient that is not normalized. In the special case of two ellipsoids, the proposed expressions are identical to those derived previously using geometric interpretations. In order to further examine the results, numerical verifications and comparisons of the Minkowski sums between two superquadric bodies are conducted. The application for the generation of configuration space obstacles in motion planning problems is introduced and demonstrated.