Closed-Form Diffeomorphic Transformations for Time Series Alignment
Paper and Code
Jun 16, 2022
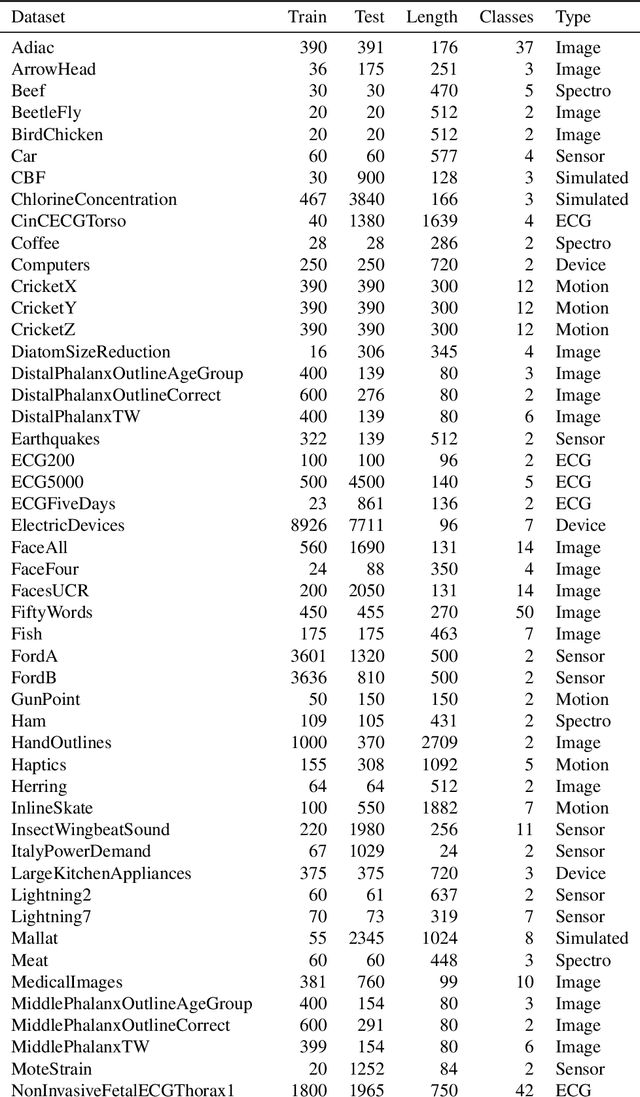
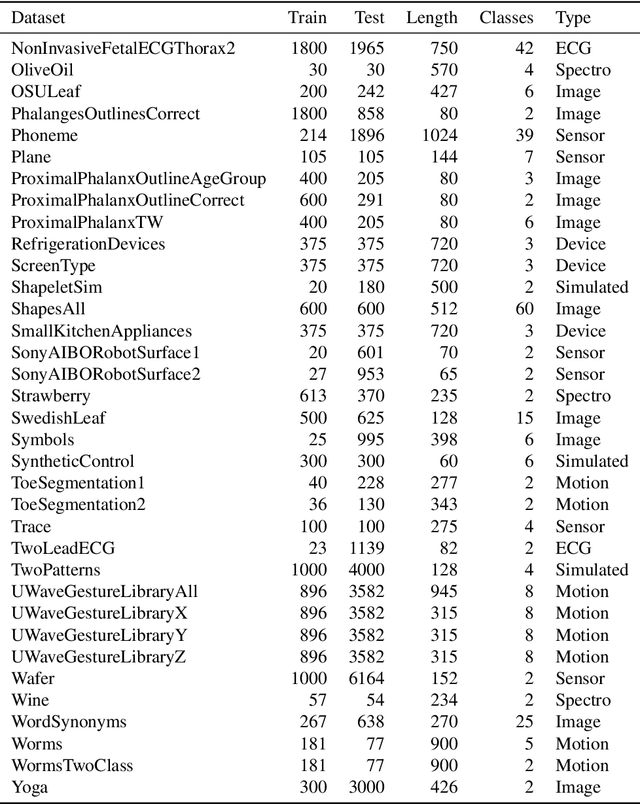

Time series alignment methods call for highly expressive, differentiable and invertible warping functions which preserve temporal topology, i.e diffeomorphisms. Diffeomorphic warping functions can be generated from the integration of velocity fields governed by an ordinary differential equation (ODE). Gradient-based optimization frameworks containing diffeomorphic transformations require to calculate derivatives to the differential equation's solution with respect to the model parameters, i.e. sensitivity analysis. Unfortunately, deep learning frameworks typically lack automatic-differentiation-compatible sensitivity analysis methods; and implicit functions, such as the solution of ODE, require particular care. Current solutions appeal to adjoint sensitivity methods, ad-hoc numerical solvers or ResNet's Eulerian discretization. In this work, we present a closed-form expression for the ODE solution and its gradient under continuous piecewise-affine (CPA) velocity functions. We present a highly optimized implementation of the results on CPU and GPU. Furthermore, we conduct extensive experiments on several datasets to validate the generalization ability of our model to unseen data for time-series joint alignment. Results show significant improvements both in terms of efficiency and accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge