Classifier Calibration: with implications to threat scores in cybersecurity

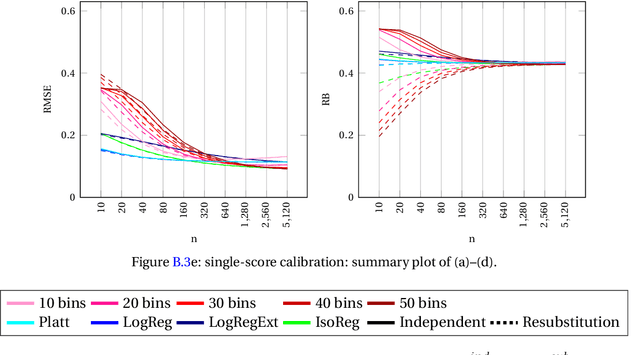
This paper explores the calibration of a classifier output score in binary classification problems. A calibrator is a function that maps the arbitrary classifier score, of a testing observation, onto $[0,1]$ to provide an estimate for the posterior probability of belonging to one of the two classes. Calibration is important for two reasons; first, it provides a meaningful score, that is the posterior probability; second, it puts the scores of different classifiers on the same scale for comparable interpretation. The paper presents three main contributions: (1) Introducing multi-score calibration, when more than one classifier provides a score for a single observation. (2) Introducing the idea that the classifier scores to a calibration process are nothing but features to a classifier, hence proposing extending the classifier scores to higher dimensions to boost the calibrator's performance. (3) Conducting a massive simulation study, in the order of 24,000 experiments, that incorporates different configurations, in addition to experimenting on two real datasets from the cybersecurity domain. The results show that there is no overall winner among the different calibrators and different configurations. However, general advices for practitioners include the following: the Platt's calibrator~\citep{Platt1999ProbabilisticOutputsForSupport}, a version of the logistic regression that decreases bias for a small sample size, has a very stable and acceptable performance among all experiments; our suggested multi-score calibration provides better performance than single score calibration in the majority of experiments, including the two real datasets. In addition, extending the scores can help in some experiments.