Classification with Sparse Overlapping Groups
Paper and Code
Sep 04, 2014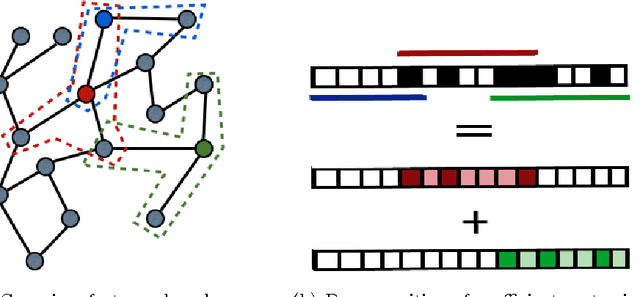


Classification with a sparsity constraint on the solution plays a central role in many high dimensional machine learning applications. In some cases, the features can be grouped together so that entire subsets of features can be selected or not selected. In many applications, however, this can be too restrictive. In this paper, we are interested in a less restrictive form of structured sparse feature selection: we assume that while features can be grouped according to some notion of similarity, not all features in a group need be selected for the task at hand. When the groups are comprised of disjoint sets of features, this is sometimes referred to as the "sparse group" lasso, and it allows for working with a richer class of models than traditional group lasso methods. Our framework generalizes conventional sparse group lasso further by allowing for overlapping groups, an additional flexiblity needed in many applications and one that presents further challenges. The main contribution of this paper is a new procedure called Sparse Overlapping Group (SOG) lasso, a convex optimization program that automatically selects similar features for classification in high dimensions. We establish model selection error bounds for SOGlasso classification problems under a fairly general setting. In particular, the error bounds are the first such results for classification using the sparse group lasso. Furthermore, the general SOGlasso bound specializes to results for the lasso and the group lasso, some known and some new. The SOGlasso is motivated by multi-subject fMRI studies in which functional activity is classified using brain voxels as features, source localization problems in Magnetoencephalography (MEG), and analyzing gene activation patterns in microarray data analysis. Experiments with real and synthetic data demonstrate the advantages of SOGlasso compared to the lasso and group lasso.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge