Classification with Partially Private Features
Paper and Code
Dec 11, 2023
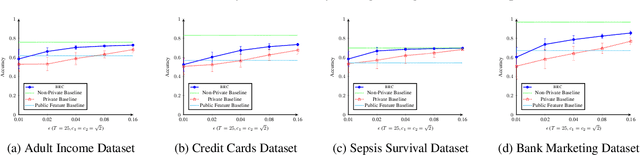
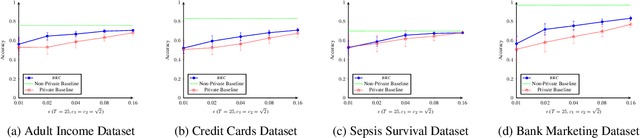
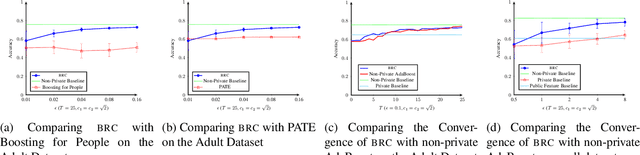
In this paper, we consider differentially private classification when some features are sensitive, while the rest of the features and the label are not. We adapt the definition of differential privacy naturally to this setting. Our main contribution is a novel adaptation of AdaBoost that is not only provably differentially private, but also significantly outperforms a natural benchmark that assumes the entire data of the individual is sensitive in the experiments. As a surprising observation, we show that boosting randomly generated classifiers suffices to achieve high accuracy. Our approach easily adapts to the classical setting where all the features are sensitive, providing an alternate algorithm for differentially private linear classification with a much simpler privacy proof and comparable or higher accuracy than differentially private logistic regression on real-world datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge