Classification Under Ambiguity: When Is Average-K Better Than Top-K?
Paper and Code
Dec 16, 2021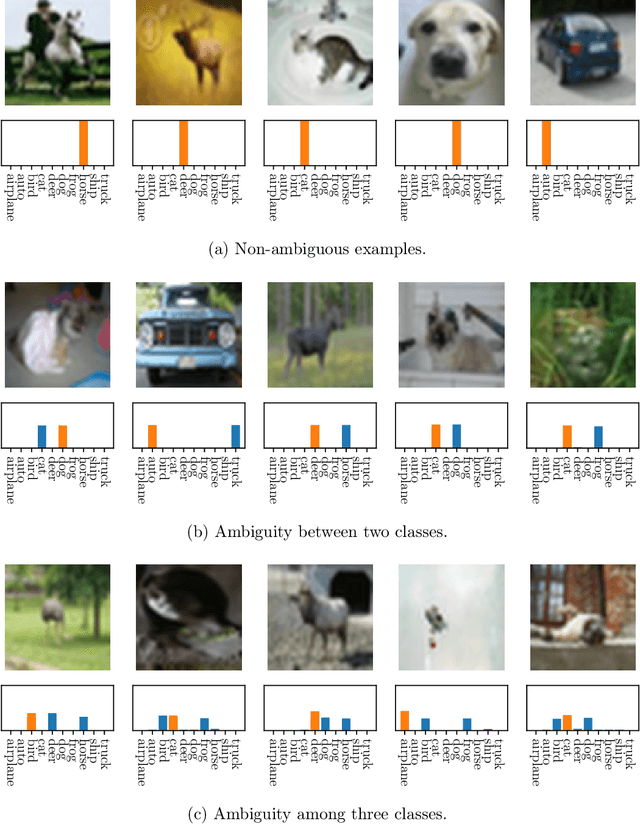

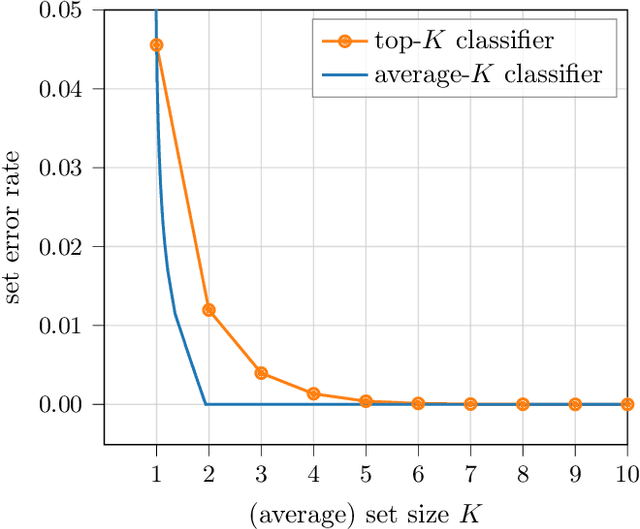
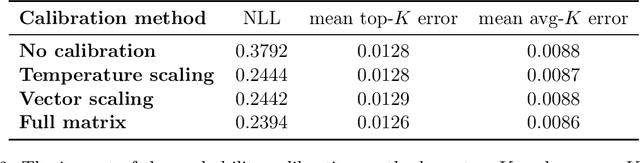
When many labels are possible, choosing a single one can lead to low precision. A common alternative, referred to as top-$K$ classification, is to choose some number $K$ (commonly around 5) and to return the $K$ labels with the highest scores. Unfortunately, for unambiguous cases, $K>1$ is too many and, for very ambiguous cases, $K \leq 5$ (for example) can be too small. An alternative sensible strategy is to use an adaptive approach in which the number of labels returned varies as a function of the computed ambiguity, but must average to some particular $K$ over all the samples. We denote this alternative average-$K$ classification. This paper formally characterizes the ambiguity profile when average-$K$ classification can achieve a lower error rate than a fixed top-$K$ classification. Moreover, it provides natural estimation procedures for both the fixed-size and the adaptive classifier and proves their consistency. Finally, it reports experiments on real-world image data sets revealing the benefit of average-$K$ classification over top-$K$ in practice. Overall, when the ambiguity is known precisely, average-$K$ is never worse than top-$K$, and, in our experiments, when it is estimated, this also holds.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge