ChebNet: Efficient and Stable Constructions of Deep Neural Networks with Rectified Power Units using Chebyshev Approximations

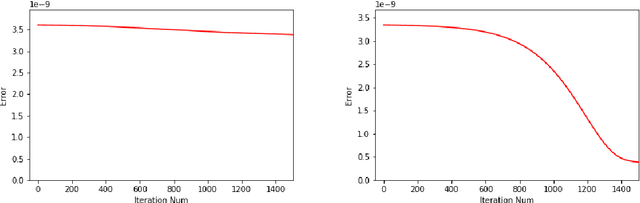
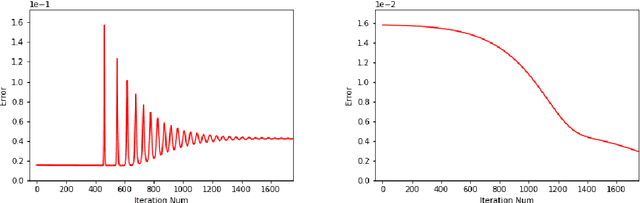
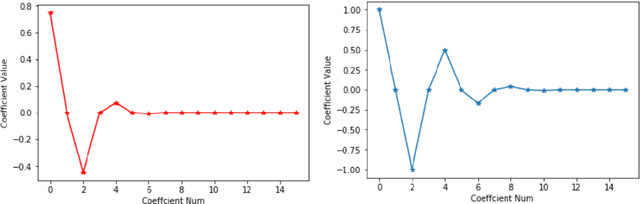
In a recent paper [B. Li, S. Tang and H. Yu, arXiv:1903.05858], it was shown that deep neural networks built with rectified power units (RePU) can give better approximation for sufficient smooth functions than those with rectified linear units, by converting polynomial approximation given in power series into deep neural networks with optimal complexity and no approximation error. However, in practice, power series are not easy to compute. In this paper, we propose a new and more stable way to construct deep RePU neural networks based on Chebyshev polynomial approximations. By using a hierarchical structure of Chebyshev polynomial approximation in frequency domain, we build efficient and stable deep neural network constructions. In theory, ChebNets and the deep RePU nets based on Power series have the same upper error bounds for general function approximations. But numerically, ChebNets are much more stable. Numerical results show that the constructed ChebNets can be further trained and obtain much better results than those obtained by training deep RePU nets constructed basing on power series.