CHARME: A chain-based reinforcement learning approach for the minor embedding problem
Paper and Code
Jun 11, 2024
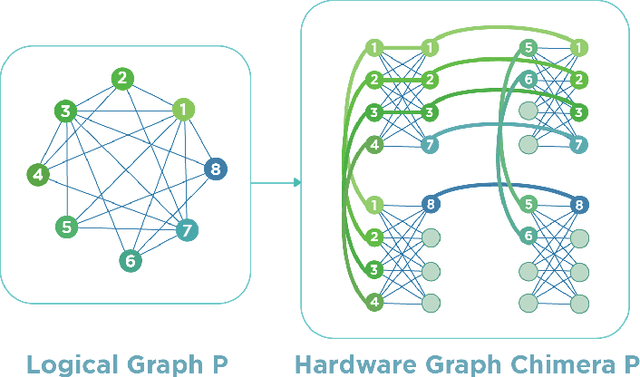
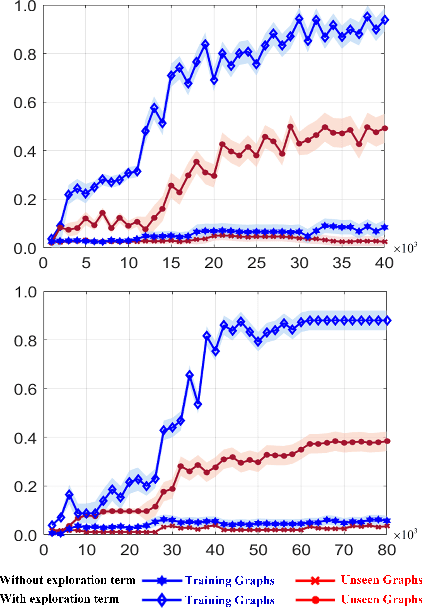

Quantum Annealing (QA) holds great potential for solving combinatorial optimization problems efficiently. However, the effectiveness of QA algorithms heavily relies on the embedding of problem instances, represented as logical graphs, into the quantum unit processing (QPU) whose topology is in form of a limited connectivity graph, known as the minor embedding Problem. Existing methods for the minor embedding problem suffer from scalability issues when confronted with larger problem sizes. In this paper, we propose a novel approach utilizing Reinforcement Learning (RL) techniques to address the minor embedding problem, named CHARME. CHARME includes three key components: a Graph Neural Network (GNN) architecture for policy modeling, a state transition algorithm ensuring solution validity, and an order exploration strategy for effective training. Through comprehensive experiments on synthetic and real-world instances, we demonstrate that the efficiency of our proposed order exploration strategy as well as our proposed RL framework, CHARME. In details, CHARME yields superior solutions compared to fast embedding methods such as Minorminer and ATOM. Moreover, our method surpasses the OCT-based approach, known for its slower runtime but high-quality solutions, in several cases. In addition, our proposed exploration enhances the efficiency of the training of the CHARME framework by providing better solutions compared to the greedy strategy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge