Characterizing how 'distributional' NLP corpora distance metrics are
Paper and Code
Oct 23, 2023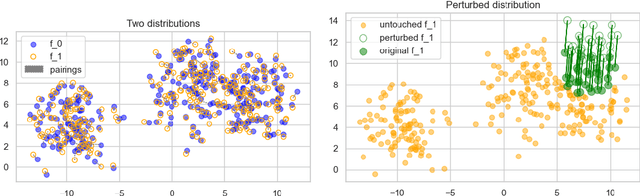
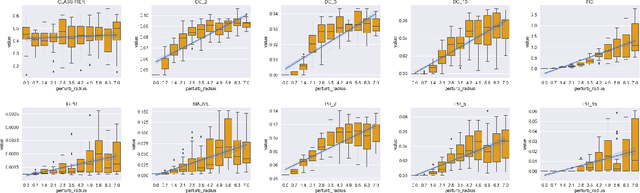
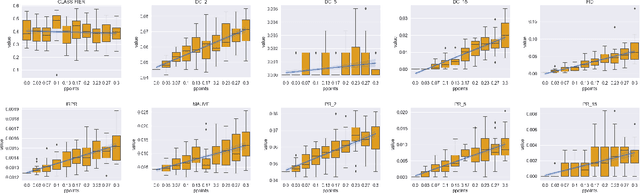
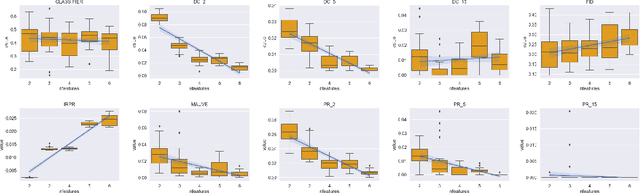
A corpus of vector-embedded text documents has some empirical distribution. Given two corpora, we want to calculate a single metric of distance (e.g., Mauve, Frechet Inception) between them. We describe an abstract quality, called `distributionality', of such metrics. A non-distributional metric tends to use very local measurements, or uses global measurements in a way that does not fully reflect the distributions' true distance. For example, if individual pairwise nearest-neighbor distances are low, it may judge the two corpora to have low distance, even if their two distributions are in fact far from each other. A more distributional metric will, in contrast, better capture the distributions' overall distance. We quantify this quality by constructing a Known-Similarity Corpora set from two paraphrase corpora and calculating the distance between paired corpora from it. The distances' trend shape as set element separation increases should quantify the distributionality of the metric. We propose that Average Hausdorff Distance and energy distance between corpora are representative examples of non-distributional and distributional distance metrics, to which other metrics can be compared, to evaluate how distributional they are.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge