Cause-Effect Deep Information Bottleneck For Incomplete Covariates
Paper and Code
Oct 08, 2018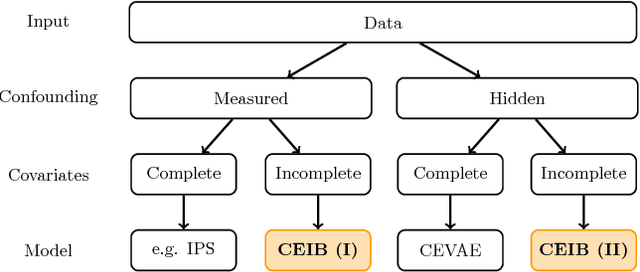


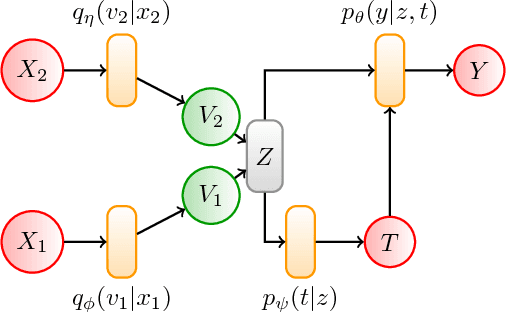
Estimating the causal effects of an intervention in the presence of confounding is a frequently occurring problem in applications such as medicine. The task is challenging since there may be multiple confounding factors, some of which may be missing, and inferences must be made from high-dimensional, noisy measurements. In this paper, we propose a decision-theoretic approach to estimate the causal effects of interventions where a subset of the covariates is unavailable for some patients during testing. Our approach uses the information bottleneck principle to perform a discrete, low-dimensional sufficient reduction of the covariate data to estimate a distribution over confounders. In doing so, we can estimate the causal effect of an intervention where only partial covariate information is available. Our results on a causal inference benchmark and a real application for treating sepsis show that our method achieves state-of-the-art performance, without sacrificing interpretability.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge