Causal Discovery by Telling Apart Parents and Children
Paper and Code
Sep 06, 2018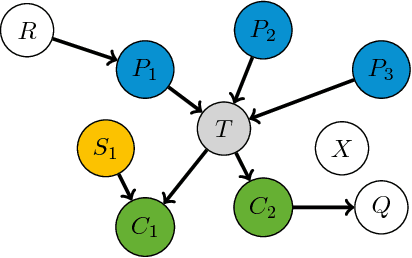
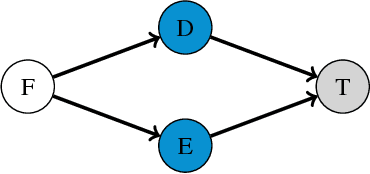
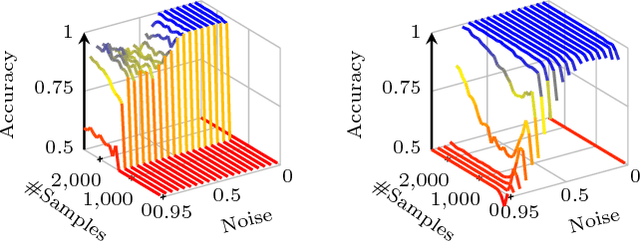
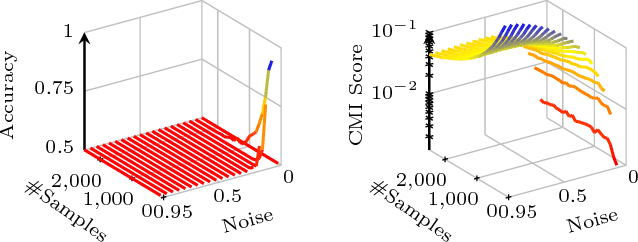
We consider the problem of inferring the directed, causal graph from observational data, assuming no hidden confounders. We take an information theoretic approach, and make three main contributions. First, we show how through algorithmic information theory we can obtain SCI, a highly robust, effective and computationally efficient test for conditional independence---and show it outperforms the state of the art when applied in constraint-based inference methods such as stable PC. Second, building upon on SCI, we show how to tell apart the parents and children of a given node based on the algorithmic Markov condition. We give the Climb algorithm to efficiently discover the directed, causal Markov blanket---and show it is at least as accurate as inferring the global network, while being much more efficient. Last, but not least, we detail how we can use the Climb score to direct those edges that state of the art causal discovery algorithms based on PC or GES leave undirected---and show this improves their precision, recall and F1 scores by up to 20%.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge