Cascading Failures in Smart Grids under Random, Targeted and Adaptive Attacks
Paper and Code
Jun 25, 2022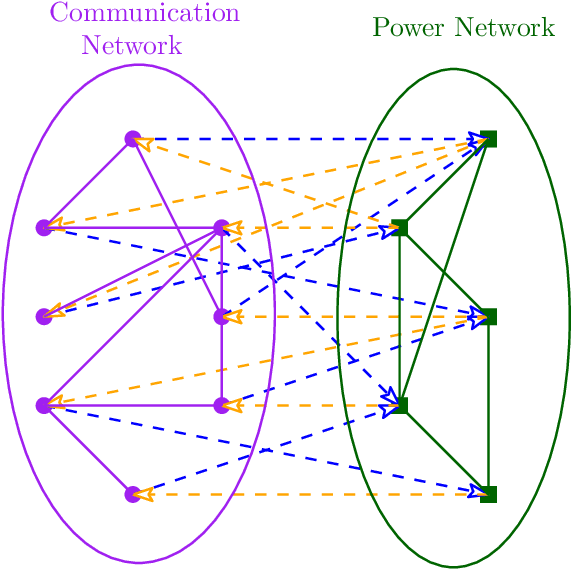
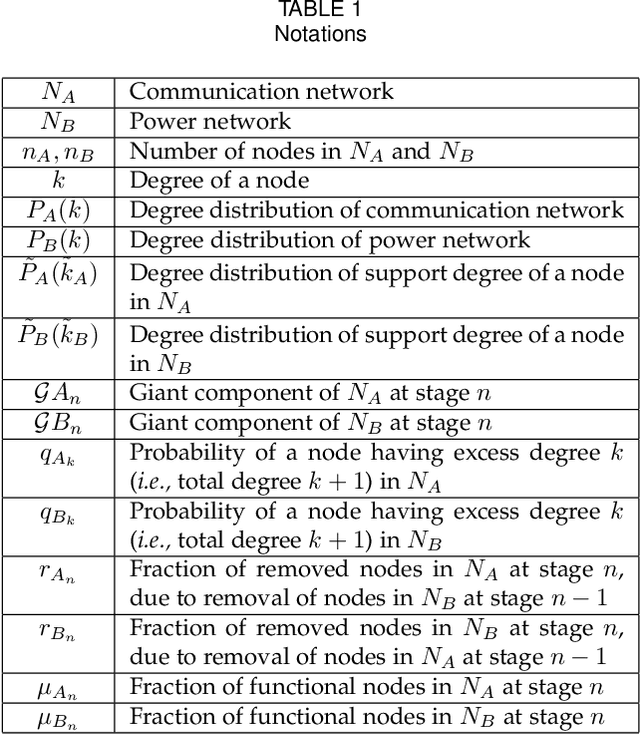
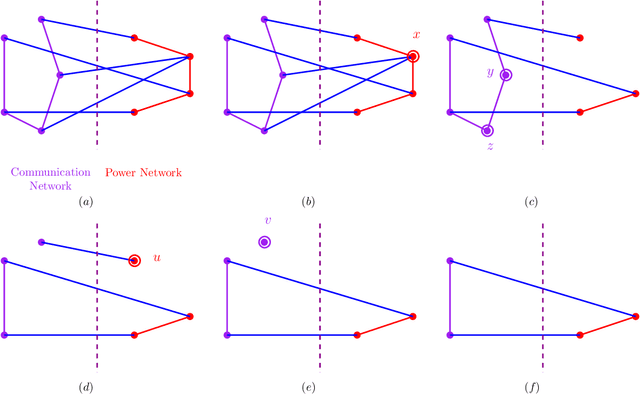
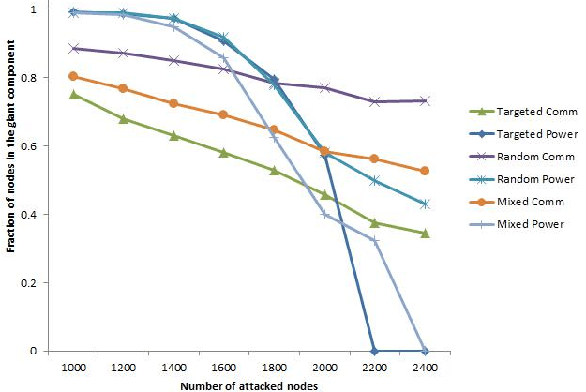
We study cascading failures in smart grids, where an attacker selectively compromises the nodes with probabilities proportional to their degrees, betweenness, or clustering coefficient. This implies that nodes with high degrees, betweenness, or clustering coefficients are attacked with higher probability. We mathematically and experimentally analyze the sizes of the giant components of the networks under different types of targeted attacks, and compare the results with the corresponding sizes under random attacks. We show that networks disintegrate faster for targeted attacks compared to random attacks. A targeted attack on a small fraction of high degree nodes disintegrates one or both of the networks, whereas both the networks contain giant components for random attack on the same fraction of nodes. An important observation is that an attacker has an advantage if it compromises nodes based on their betweenness, rather than based on degree or clustering coefficient. We next study adaptive attacks, where an attacker compromises nodes in rounds. Here, some nodes are compromised in each round based on their degree, betweenness or clustering coefficients, instead of compromising all nodes together. In this case, the degree, betweenness, or clustering coefficient is calculated before the start of each round, instead of at the beginning. We show experimentally that an adversary has an advantage in this adaptive approach, compared to compromising the same number of nodes all at once.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge