Can graph neural networks count substructures?

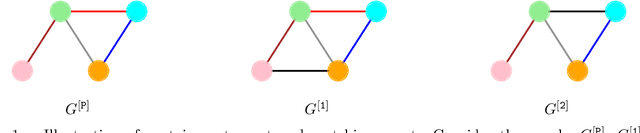
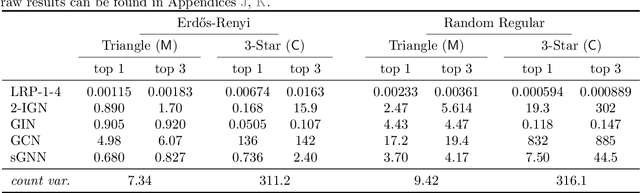
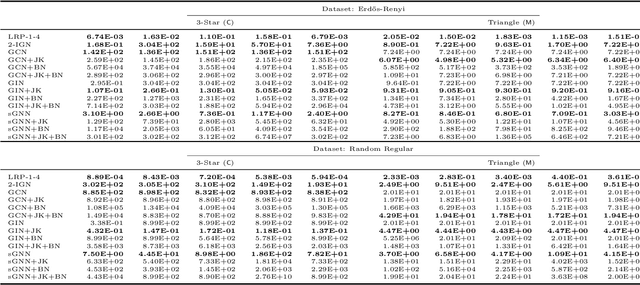
The ability to detect and count certain substructures in graphs is important for solving many tasks on graph-structured data, especially in the contexts of computational chemistry and biology as well as social network analysis. Inspired by this, we propose to study the expressive power of graph neural networks (GNNs) via their ability to count attributed graph substructures, extending recent works that examine their power in graph isomorphism testing and function approximation. We distinguish between two types of substructure counting: matching-count and containment-count, and establish both positive and negative answers for popular GNN architectures. Specifically, we prove that Message Passing Neural Networks (MPNNs), 2-Weisfeiler-Lehman (2-WL) and 2-Invariant Graph Networks (2-IGNs) cannot perform matching-count of substructures consisting of 3 or more nodes, while they can perform containment-count of star-shaped substructures. We also prove positive results for k-WL and k-IGNs as well as negative results for k-WL with limited number of iterations. We then conduct experiments that support the theoretical results for MPNNs and 2-IGNs, and demonstrate that local relational pooling strategies inspired by Murphy et al. (2019) are more effective for substructure counting. In addition, as an intermediary step, we prove that 2-WL and 2-IGNs are equivalent in distinguishing non-isomorphic graphs, partly answering an open problem raised in Maron et al. (2019).