Calibration of Shared Equilibria in General Sum Partially Observable Markov Games

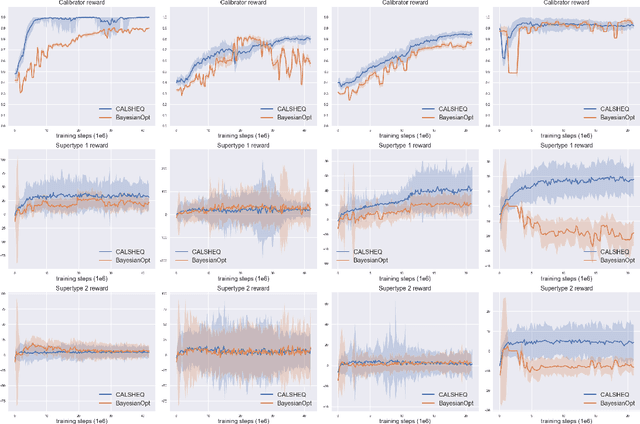
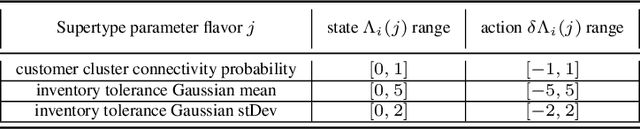
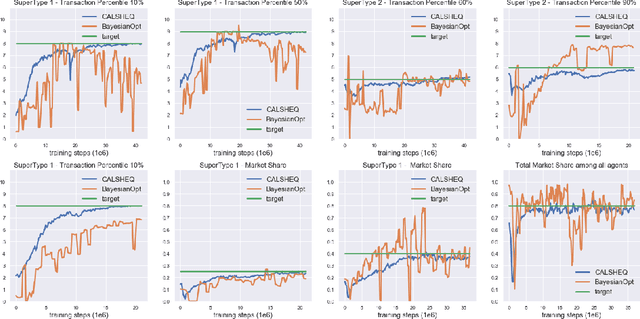
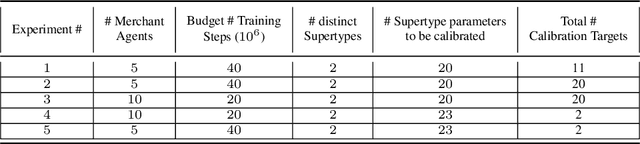
Training multi-agent systems (MAS) to achieve realistic equilibria gives us a useful tool to understand and model real-world systems. We consider a general sum partially observable Markov game where agents of different types share a single policy network, conditioned on agent-specific information. This paper aims at i) formally understanding equilibria reached by such agents, and ii) matching emergent phenomena of such equilibria to real-world targets. Parameter sharing with decentralized execution has been introduced as an efficient way to train multiple agents using a single policy network. However, the nature of resulting equilibria reached by such agents is not yet understood: we introduce the novel concept of \textit{Shared equilibrium} as a symmetric pure Nash equilibrium of a certain Functional Form Game (FFG) and prove convergence to the latter for a certain class of games using self-play. In addition, it is important that such equilibria satisfy certain constraints so that MAS are \textit{calibrated} to real world data for practical use: we solve this problem by introducing a novel dual-Reinforcement Learning based approach that fits emergent behaviors of agents in a Shared equilibrium to externally-specified targets, and apply our methods to a $n$-player market example. We do so by calibrating parameters governing distributions of agent types rather than individual agents, which allows both behavior differentiation among agents and coherent scaling of the shared policy network to multiple agents.