c-TPE: Generalizing Tree-structured Parzen Estimator with Inequality Constraints for Continuous and Categorical Hyperparameter Optimization

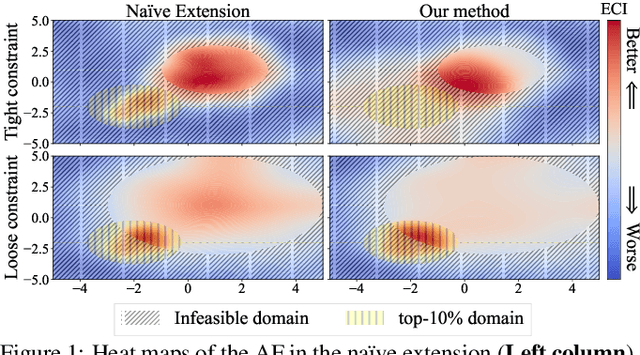
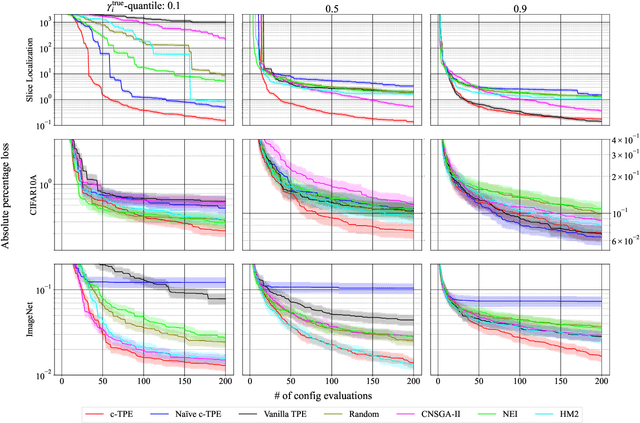
Hyperparameter optimization (HPO) is crucial for strong performance of deep learning algorithms. A widely-used versatile HPO method is a variant of Bayesian optimization called tree-structured Parzen estimator (TPE), which splits data into good and bad groups and uses the density ratio of those groups as an acquisition function (AF). However, real-world applications often have some constraints, such as memory requirements, or latency. In this paper, we present an extension of TPE to constrained optimization (c-TPE) via simple factorization of AFs. The experiments demonstrate c-TPE is robust to various constraint levels and exhibits the best average rank performance among existing methods with statistical significance on search spaces with categorical parameters on 81 settings.