ByRDiE: Byzantine-resilient distributed coordinate descent for decentralized learning

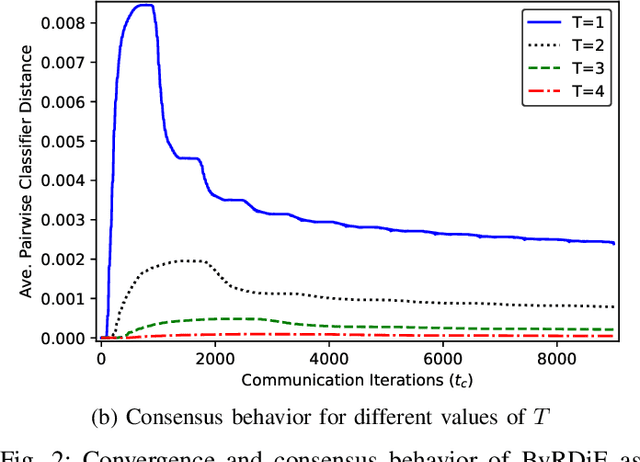
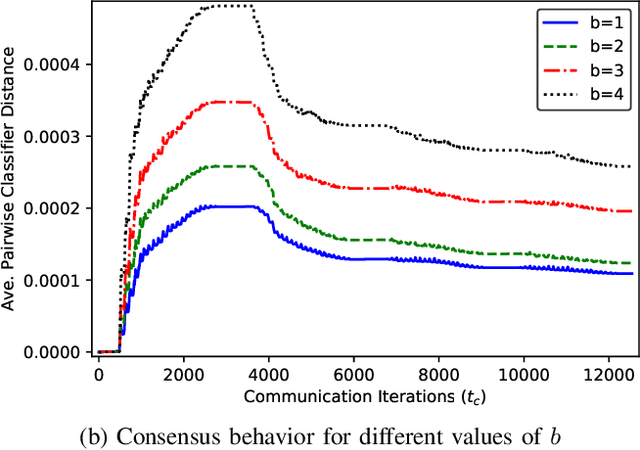
Distributed machine learning algorithms enable learning of models from datasets that are distributed over a network without gathering the data at a centralized location. While efficient distributed algorithms have been developed under the assumption of faultless networks, failures that can render these algorithms nonfunctional occur frequently in the real world. This paper focuses on the problem of Byzantine failures, which are the hardest to safeguard against in distributed algorithms. While Byzantine fault tolerance has a rich history, existing work does not translate into efficient and practical algorithms for high-dimensional distributed learning. In this paper, two variants of an algorithm termed \emph{Byzantine-resilient distributed coordinate descent} (ByRDiE) are developed and analyzed that enable distributed learning in the presence of Byzantine failures. Theoretical analysis and numerical experiments presented in the paper highlight the usefulness of ByRDiE for high-dimensional distributed learning in the presence of Byzantine failures.