But How Does It Work in Theory? Linear SVM with Random Features
Paper and Code
Sep 12, 2018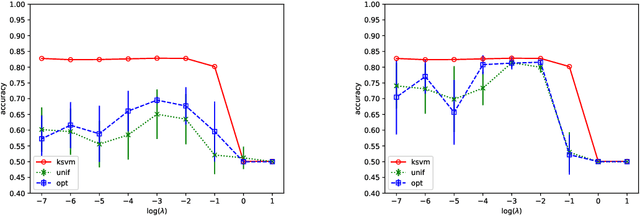
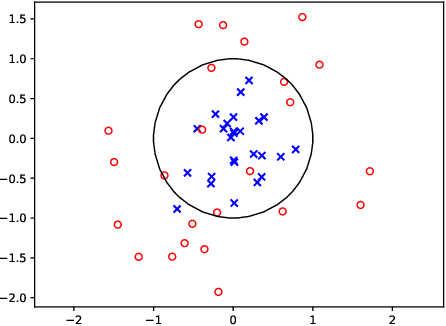
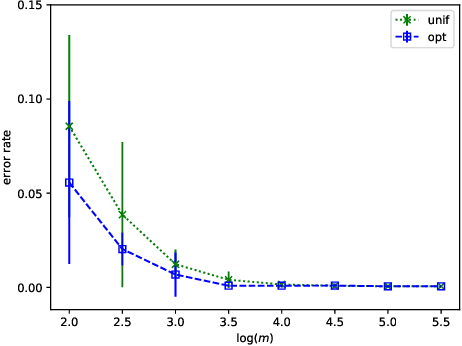
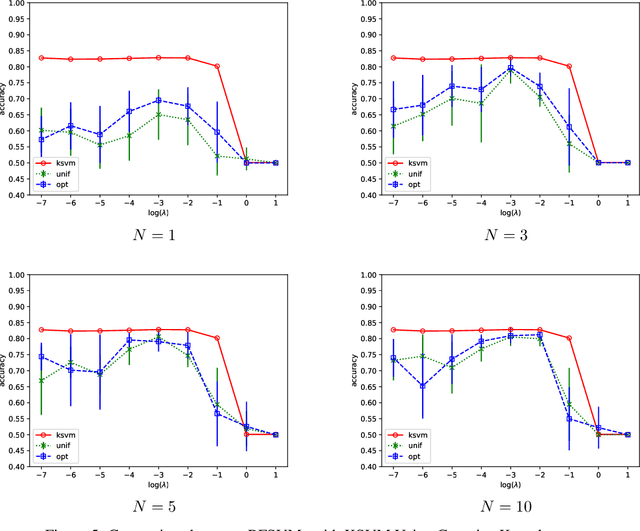
We prove that, under low noise assumptions, the support vector machine with $N\ll m$ random features (RFSVM) can achieve the learning rate faster than $O(1/\sqrt{m})$ on a training set with $m$ samples when an optimized feature map is used. Our work extends the previous fast rate analysis of random features method from least square loss to 0-1 loss. We also show that the reweighted feature selection method, which approximates the optimized feature map, helps improve the performance of RFSVM in experiments on a synthetic data set.
* Accepted by NIPS2018
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge