Bounds for the VC Dimension of 1NN Prototype Sets
Paper and Code
Feb 07, 2019
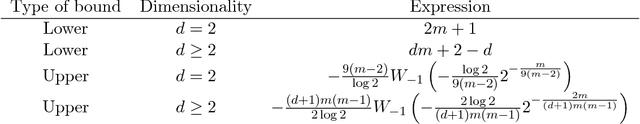
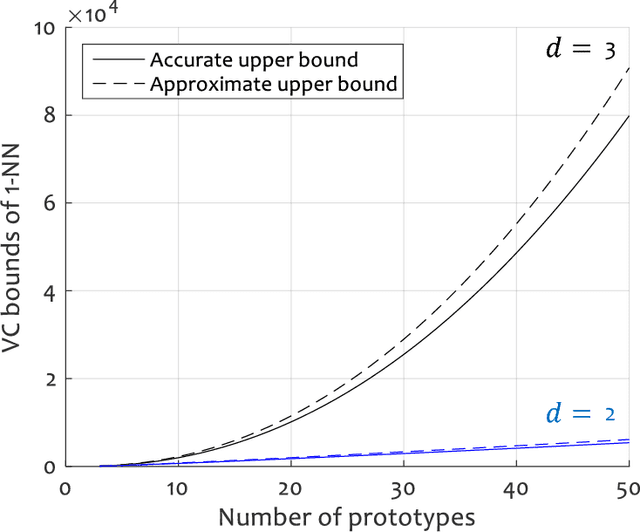
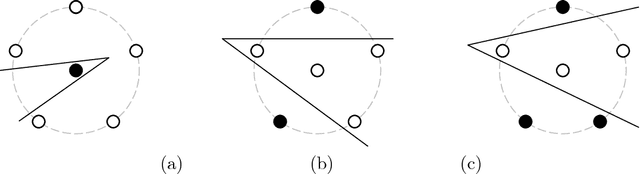
In Statistical Learning, the Vapnik-Chervonenkis (VC) dimension is an important combinatorial property of classifiers. To our knowledge, no theoretical results yet exist for the VC dimension of edited nearest-neighbour (1NN) classifiers with reference set of fixed size. Related theoretical results are scattered in the literature and their implications have not been made explicit. We collect some relevant results and use them to provide explicit lower and upper bounds for the VC dimension of 1NN classifiers with a prototype set of fixed size. We discuss the implications of these bounds for the size of training set needed to learn such a classifier to a given accuracy. Further, we provide a new lower bound for the two-dimensional case, based on a new geometrical argument.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge