Block-Coordinate Descent on the Riemannian Staircase for Certifiably Correct Distributed Rotation and Pose Synchronization

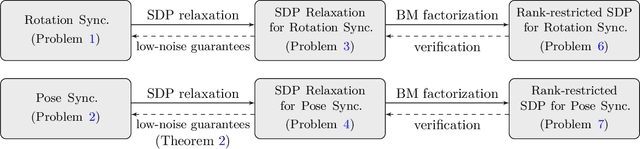
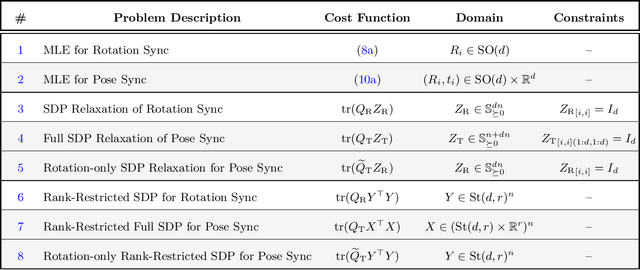
This paper presents the first certifiably correct solver for distributed rotation and pose synchronization, the backbone of modern collaborative simultaneous localization and mapping (CSLAM) and camera network localization (CNL) systems. By pursuing a sparse semidefinite relaxation, our approach provides formal performance guarantees that match the state of the art in the centralized setting. In particular, we prove that under "low" noise, the solution to the semidefinite relaxation is guaranteed to provide a globally optimal solution to the original non-convex problem. To solve the resulting large-scale semidefinite programs, we adopt the state-of-the-art Riemannian Staircase framework and develop Riemannian block-coordinate descent (RBCD) as the core distributed local search algorithm. RBCD is well-suited to distributed synchronization problems as it only requires local communication, provides privacy protection, and is easily parallelizable. Furthermore, we prove that RBCD converges to first-order critical points for general Riemannian optimization problems over product of matrix submanifolds, with a global sublinear convergence rate. Extensive evaluations on real and synthetic datasets demonstrate that the proposed solver correctly recovers globally optimal solutions under low-to-moderate noise, and outperforms alternative distributed techniques in terms of solution precision and convergence speed.