Blind Channel Equalization Using Vector-Quantized Variational Autoencoders
Paper and Code
Feb 22, 2023
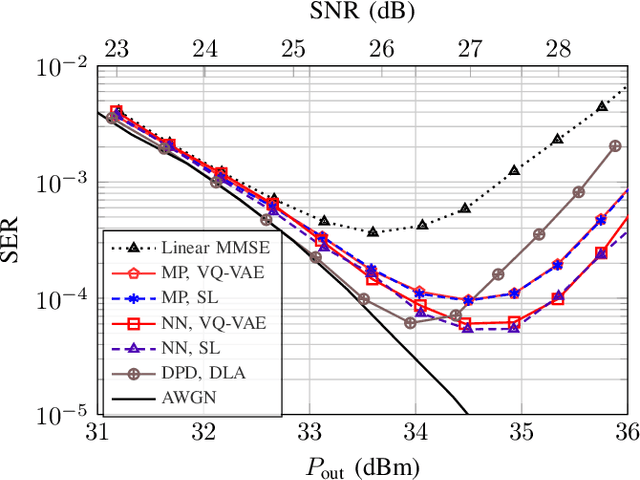
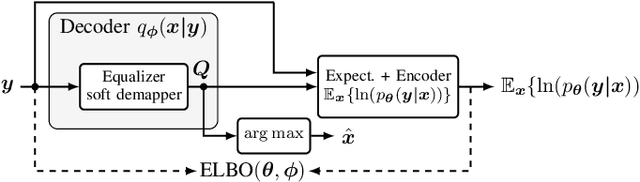

State-of-the-art high-spectral-efficiency communication systems employ high-order modulation formats coupled with high symbol rates to accommodate the ever-growing demand for data rate-hungry applications. However, such systems are more vulnerable to linear and nonlinear transmission impairments, and it is important to mitigate the performance loss via digital signal processing. In this paper, we propose a novel machine learning approach for blind channel equalization and estimation using the vector quantized (VQ) \ac{VAE} framework. The proposed approach generalizes the applicability of the conventional \ac{VAE}-based equalizer to nonlinear systems employing high-order modulation formats by introducing a codebook component and an associated novel loss function. We evaluate the performance of the proposed method over a linear additive white Gaussian noise channel with intersymbol interference and two nonlinear scenarios. Simulation results show that the proposed method can achieve similar performance as a data aided equalizer using the \acf{MMSE} criterion, and outperforms the blind\ac{CMA} and the \ac{VAE}-based channel equalizer. Furthermore, we show that for the linear channel, the proposed scheme exhibits better convergence properties than the \ac{MMSE}-based, the \ac{CMA}-based, and the \ac{VAE}-based equalizers in terms of both convergence speed and robustness to variations in training batch size and learning rate.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge