BigCarl: Mining frequent subnets from a single large Petri net
Paper and Code
Mar 21, 2021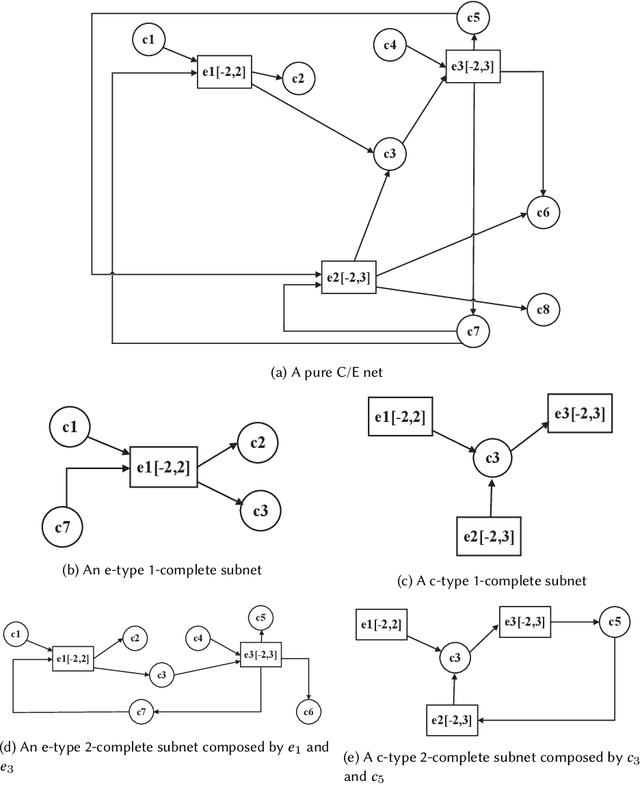

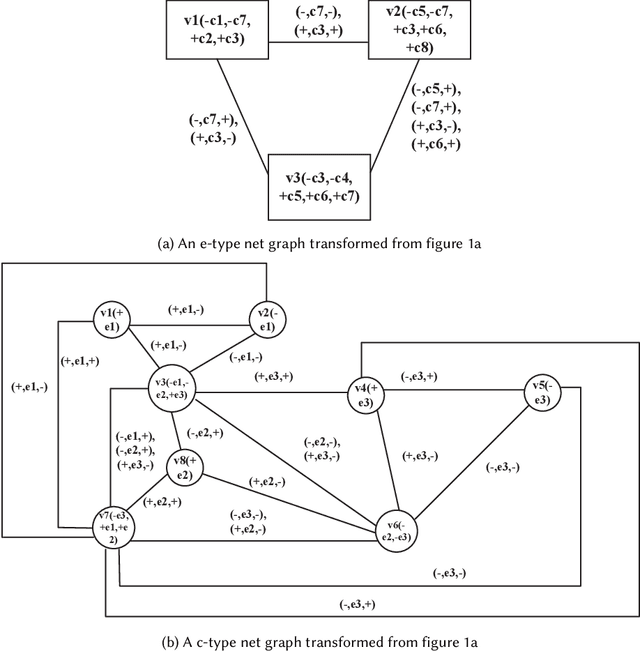
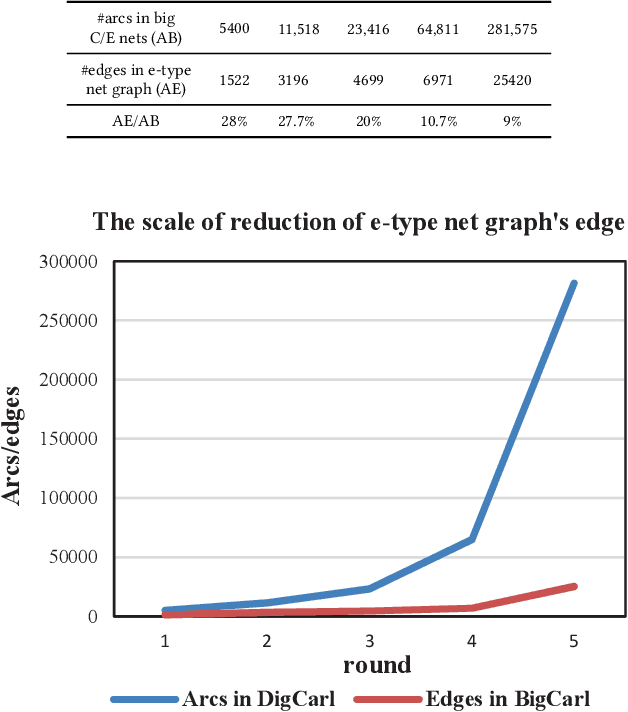
While there have been lots of work studying frequent subgraph mining, very rare publications have discussed frequent subnet mining from more complicated data structures such as Petri nets. This paper studies frequent subnets mining from a single large Petri net. We follow the idea of transforming a Petri net in net graph form and to mine frequent sub-net graphs to avoid high complexity. Technically, we take a minimal traversal approach to produce a canonical label of the big net graph. We adapted the maximal independent embedding set approach to the net graph representation and proposed an incremental pattern growth (independent embedding set reduction) way for discovering frequent sub-net graphs from the single large net graph, which are finally transformed back to frequent subnets. Extensive performance studies made on a single large Petri net, which contains 10K events, 40K conditions and 30 K arcs, showed that our approach is correct and the complexity is reasonable.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge