Bidirectional Consistency Models
Paper and Code
Mar 30, 2024
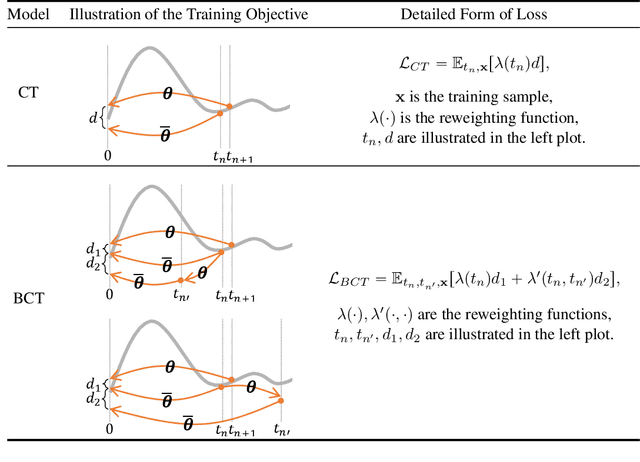

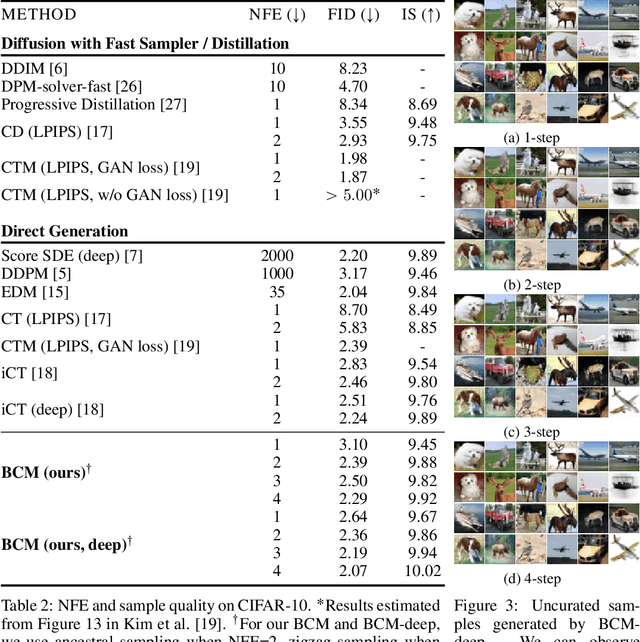
Diffusion models (DMs) are capable of generating remarkably high-quality samples by iteratively denoising a random vector, a process that corresponds to moving along the probability flow ordinary differential equation (PF ODE). Interestingly, DMs can also invert an input image to noise by moving backward along the PF ODE, a key operation for downstream tasks such as interpolation and image editing. However, the iterative nature of this process restricts its speed, hindering its broader application. Recently, Consistency Models (CMs) have emerged to address this challenge by approximating the integral of the PF ODE, largely reducing the number of iterations. Yet, the absence of an explicit ODE solver complicates the inversion process. To resolve this, we introduce the Bidirectional Consistency Model (BCM), which learns a single neural network that enables both forward and backward traversal along the PF ODE, efficiently unifying generation and inversion tasks within one framework. Notably, our proposed method enables one-step generation and inversion while also allowing the use of additional steps to enhance generation quality or reduce reconstruction error. Furthermore, by leveraging our model's bidirectional consistency, we introduce a sampling strategy that can enhance FID while preserving the generated image content. We further showcase our model's capabilities in several downstream tasks, such as interpolation and inpainting, and present demonstrations of potential applications, including blind restoration of compressed images and defending black-box adversarial attacks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge