Beyond 1-WL with Local Ego-Network Encodings
Paper and Code
Dec 07, 2022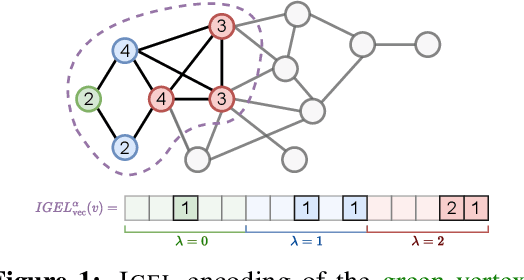
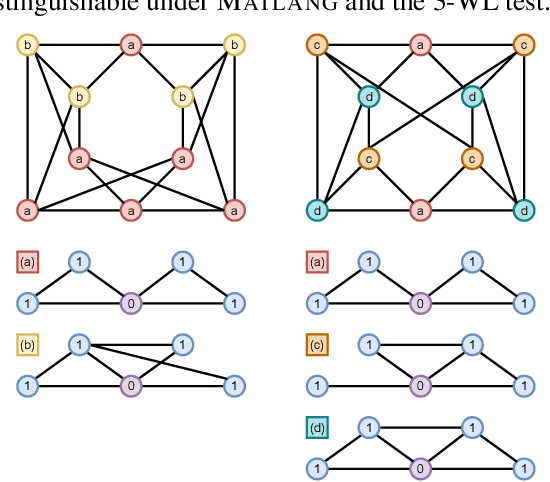
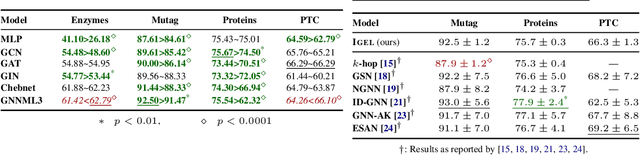
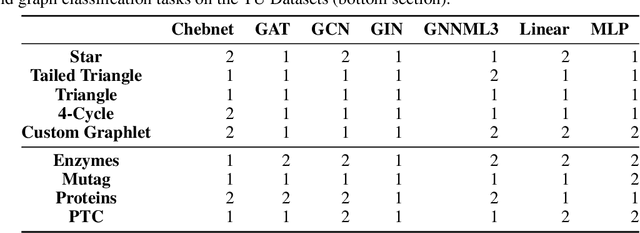
Identifying similar network structures is key to capture graph isomorphisms and learn representations that exploit structural information encoded in graph data. This work shows that ego-networks can produce a structural encoding scheme for arbitrary graphs with greater expressivity than the Weisfeiler-Lehman (1-WL) test. We introduce IGEL, a preprocessing step to produce features that augment node representations by encoding ego-networks into sparse vectors that enrich Message Passing (MP) Graph Neural Networks (GNNs) beyond 1-WL expressivity. We describe formally the relation between IGEL and 1-WL, and characterize its expressive power and limitations. Experiments show that IGEL matches the empirical expressivity of state-of-the-art methods on isomorphism detection while improving performance on seven GNN architectures.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge