Bayesian Variational Optimization for Combinatorial Spaces
Paper and Code
Nov 03, 2020
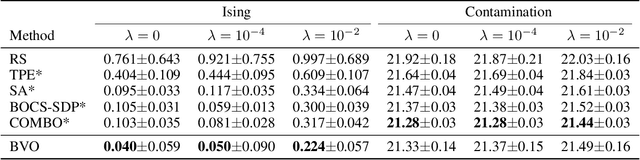
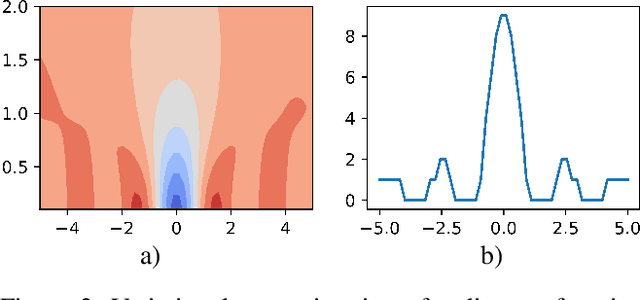
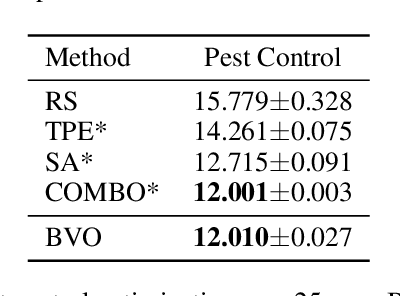
This paper focuses on Bayesian Optimization in combinatorial spaces. In many applications in the natural science. Broad applications include the study of molecules, proteins, DNA, device structures and quantum circuit designs, a on optimization over combinatorial categorical spaces is needed to find optimal or pareto-optimal solutions. However, only a limited amount of methods have been proposed to tackle this problem. Many of them depend on employing Gaussian Process for combinatorial Bayesian Optimizations. Gaussian Processes suffer from scalability issues for large data sizes as their scaling is cubic with respect to the number of data points. This is often impractical for optimizing large search spaces. Here, we introduce a variational Bayesian optimization method that combines variational optimization and continuous relaxations to the optimization of the acquisition function for Bayesian optimization. Critically, this method allows for gradient-based optimization and has the capability of optimizing problems with large data size and data dimensions. We have shown the performance of our method is comparable to state-of-the-art methods while maintaining its scalability advantages. We also applied our method in molecular optimization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge