Bayesian ODE Solvers: The Maximum A Posteriori Estimate
Paper and Code
Apr 01, 2020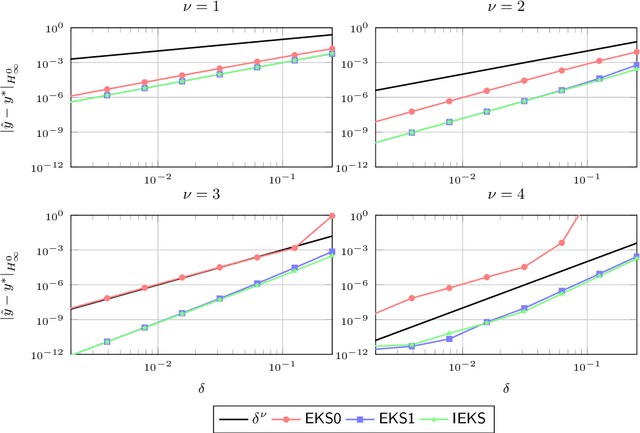
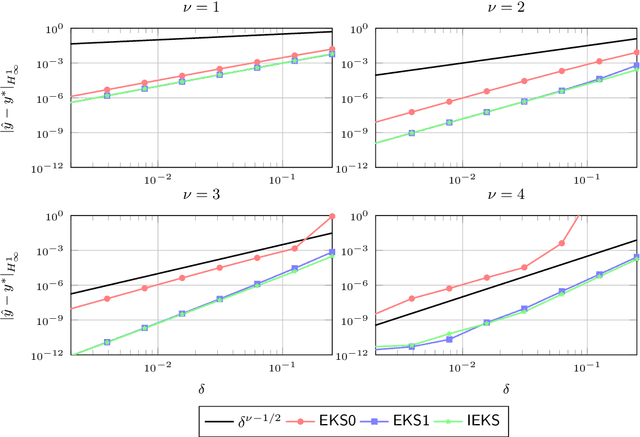
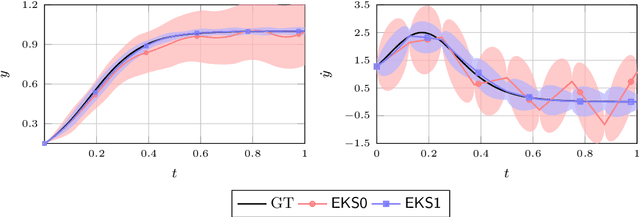
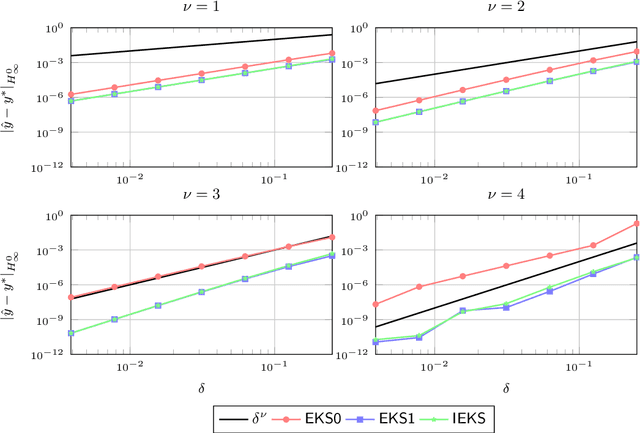
It has recently been established that the numerical solution of ordinary differential equations can be posed as a nonlinear Bayesian inference problem, which can be approximately solved via Gaussian filtering and smoothing, whenever a Gauss--Markov prior is used. In this paper the class of $\nu$ times differentiable linear time invariant Gauss--Markov priors is considered. A taxonomy of Gaussian estimators is established, with the maximum a posteriori estimate at the top of the hierarchy, which can be computed with the iterated extended Kalman smoother. The remaining three classes are termed explicit, semi-implicit, and implicit, which are in similarity with the classical notions corresponding to conditions on the vector field, under which the filter update produces a local maximum a posteriori estimate. The maximum a posteriori estimate corresponds to an optimal interpolant in the reproducing Hilbert space associated with the prior, which in the present case is equivalent to a Sobolev space of smoothness $\nu+1$. Consequently, using methods from scattered data approximation and nonlinear analysis in Sobolev spaces, it is shown that the maximum a posteriori estimate converges to the true solution at a polynomial rate in the fill-distance (maximum step size) subject to mild conditions on the vector field. The methodology developed provides a novel and more natural approach to study the convergence of these estimators than classical methods of convergence analysis. The methods and theoretical results are demonstrated in numerical examples.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge