Bayesian differential programming for robust systems identification under uncertainty
Paper and Code
Apr 18, 2020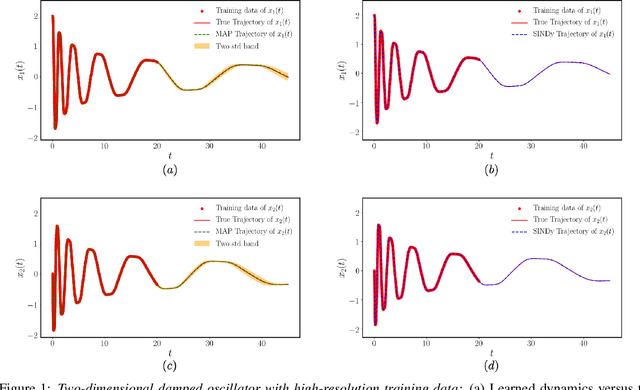
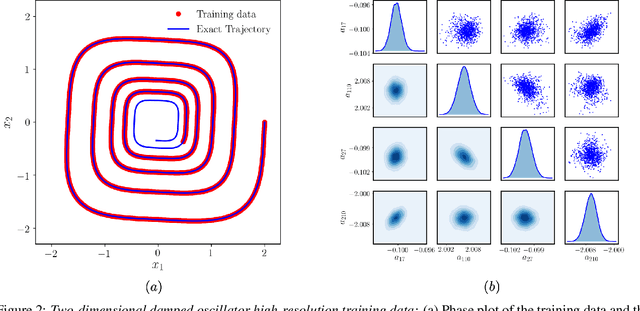

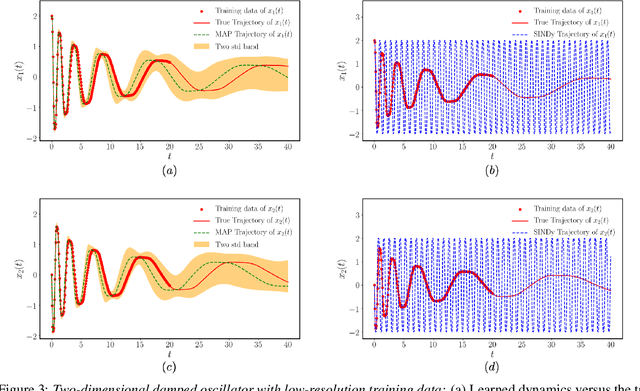
This paper presents a machine learning framework for Bayesian systems identification from noisy, sparse and irregular observations of nonlinear dynamical systems. The proposed method takes advantage of recent developments in differentiable programming to propagate gradient information through ordinary differential equation solvers and perform Bayesian inference with respect to unknown model parameters using Hamiltonian Monte Carlo. This allows us to efficiently infer posterior distributions over plausible models with quantified uncertainty, while the use of sparsity-promoting priors enables the discovery of interpretable and parsimonious representations for the underlying latent dynamics. A series of numerical studies is presented to demonstrate the effectiveness of the proposed methods including nonlinear oscillators, predator-prey systems, chaotic dynamics and systems biology. Taken all together, our findings put forth a novel, flexible and robust workflow for data-driven model discovery under uncertainty.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge