Bayesian community detection for networks with covariates
Paper and Code
Mar 04, 2022

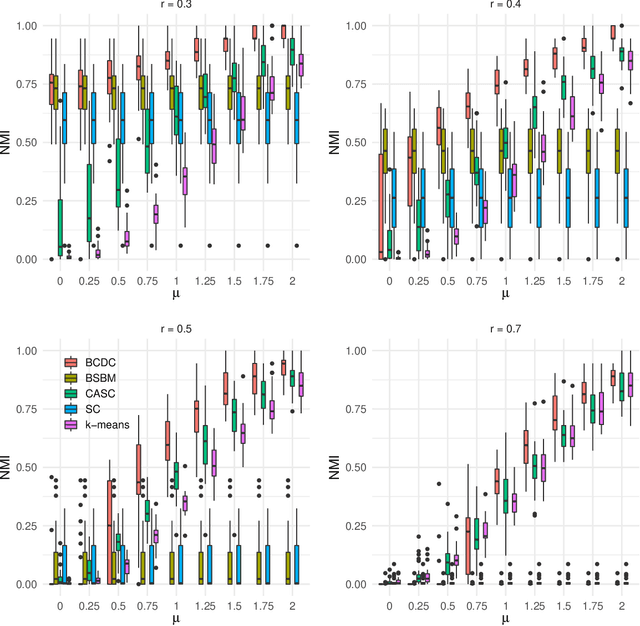

The increasing prevalence of network data in a vast variety of fields and the need to extract useful information out of them have spurred fast developments in related models and algorithms. Among the various learning tasks with network data, community detection, the discovery of node clusters or "communities," has arguably received the most attention in the scientific community. In many real-world applications, the network data often come with additional information in the form of node or edge covariates that should ideally be leveraged for inference. In this paper, we add to a limited literature on community detection for networks with covariates by proposing a Bayesian stochastic block model with a covariate-dependent random partition prior. Under our prior, the covariates are explicitly expressed in specifying the prior distribution on the cluster membership. Our model has the flexibility of modeling uncertainties of all the parameter estimates including the community membership. Importantly, and unlike the majority of existing methods, our model has the ability to learn the number of the communities via posterior inference without having to assume it to be known. Our model can be applied to community detection in both dense and sparse networks, with both categorical and continuous covariates, and our MCMC algorithm is very efficient with good mixing properties. We demonstrate the superior performance of our model over existing models in a comprehensive simulation study and an application to two real datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge