Bayesian Bellman Operators
Paper and Code
Jun 15, 2021
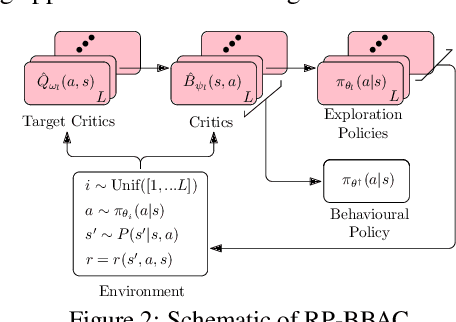


We introduce a novel perspective on Bayesian reinforcement learning (RL); whereas existing approaches infer a posterior over the transition distribution or Q-function, we characterise the uncertainty in the Bellman operator. Our Bayesian Bellman operator (BBO) framework is motivated by the insight that when bootstrapping is introduced, model-free approaches actually infer a posterior over Bellman operators, not value functions. In this paper, we use BBO to provide a rigorous theoretical analysis of model-free Bayesian RL to better understand its relationshipto established frequentist RL methodologies. We prove that Bayesian solutions are consistent with frequentist RL solutions, even when approximate inference isused, and derive conditions for which convergence properties hold. Empirically, we demonstrate that algorithms derived from the BBO framework have sophisticated deep exploration properties that enable them to solve continuous control tasks at which state-of-the-art regularised actor-critic algorithms fail catastrophically
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge