Bayesian Algorithms for Decentralized Stochastic Bandits
Paper and Code
Oct 28, 2020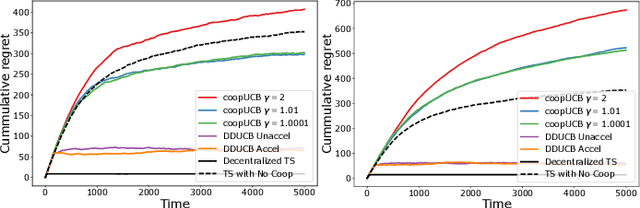
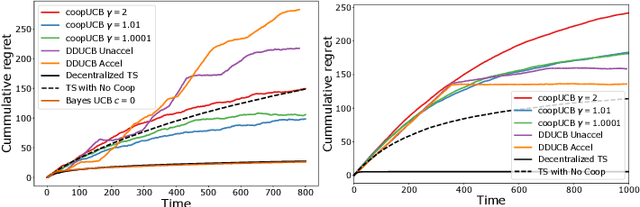
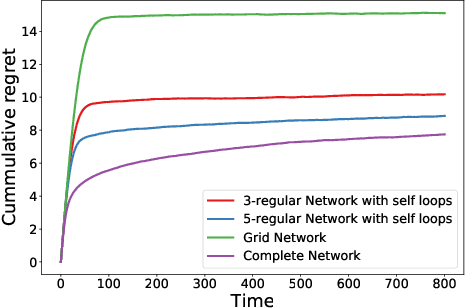
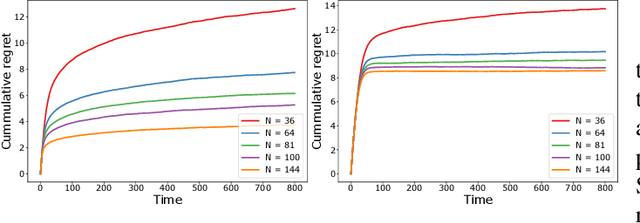
We study a decentralized cooperative multi-agent multi-armed bandit problem with $K$ arms and $N$ agents connected over a network. In our model, each arm's reward distribution is same for all agents, and rewards are drawn independently across agents and over time steps. In each round, agents choose an arm to play and subsequently send a message to their neighbors. The goal is to minimize cumulative regret averaged over the entire network. We propose a decentralized Bayesian multi-armed bandit framework that extends single-agent Bayesian bandit algorithms to the decentralized setting. Specifically, we study an information assimilation algorithm that can be combined with existing Bayesian algorithms, and using this, we propose a decentralized Thompson Sampling algorithm and decentralized Bayes-UCB algorithm. We analyze the decentralized Thompson Sampling algorithm under Bernoulli rewards and establish a problem-dependent upper bound on the cumulative regret. We show that regret incurred scales logarithmically over the time horizon with constants that match those of an optimal centralized agent with access to all observations across the network. Our analysis also characterizes the cumulative regret in terms of the network structure. Through extensive numerical studies, we show that our extensions of Thompson Sampling and Bayes-UCB incur lesser cumulative regret than the state-of-art algorithms inspired by the Upper Confidence Bound algorithm. We implement our proposed decentralized Thompson Sampling under gossip protocol, and over time-varying networks, where each communication link has a fixed probability of failure.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge