Bayesian Adversarial Spheres: Bayesian Inference and Adversarial Examples in a Noiseless Setting
Paper and Code
Nov 29, 2018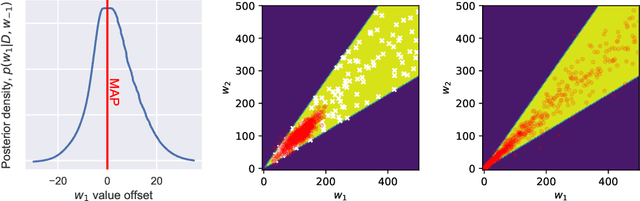
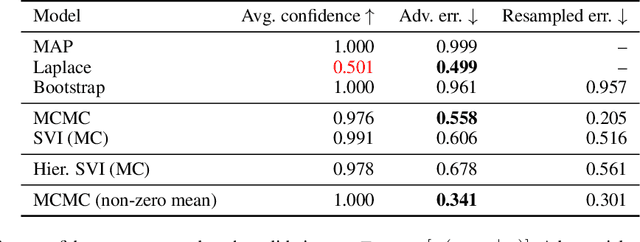
Modern deep neural network models suffer from adversarial examples, i.e. confidently misclassified points in the input space. It has been shown that Bayesian neural networks are a promising approach for detecting adversarial points, but careful analysis is problematic due to the complexity of these models. Recently Gilmer et al. (2018) introduced adversarial spheres, a toy set-up that simplifies both practical and theoretical analysis of the problem. In this work, we use the adversarial sphere set-up to understand the properties of approximate Bayesian inference methods for a linear model in a noiseless setting. We compare predictions of Bayesian and non-Bayesian methods, showcasing the advantages of the former, although revealing open challenges for deep learning applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge