Bayesian Active Learning for Censored Regression
Paper and Code
Feb 19, 2024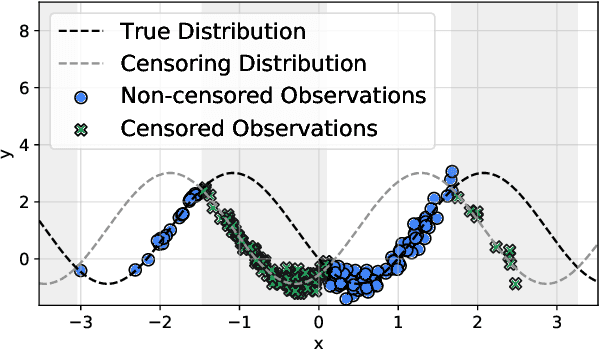

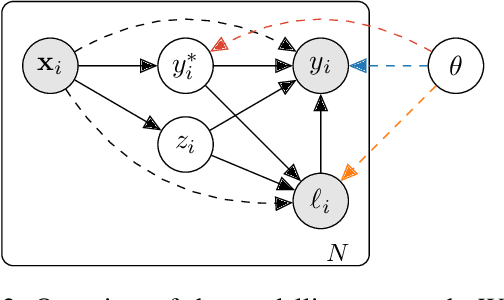

Bayesian active learning is based on information theoretical approaches that focus on maximising the information that new observations provide to the model parameters. This is commonly done by maximising the Bayesian Active Learning by Disagreement (BALD) acquisitions function. However, we highlight that it is challenging to estimate BALD when the new data points are subject to censorship, where only clipped values of the targets are observed. To address this, we derive the entropy and the mutual information for censored distributions and derive the BALD objective for active learning in censored regression ($\mathcal{C}$-BALD). We propose a novel modelling approach to estimate the $\mathcal{C}$-BALD objective and use it for active learning in the censored setting. Across a wide range of datasets and models, we demonstrate that $\mathcal{C}$-BALD outperforms other Bayesian active learning methods in censored regression.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge