Bayes-Newton Methods for Approximate Bayesian Inference with PSD Guarantees
Paper and Code
Nov 03, 2021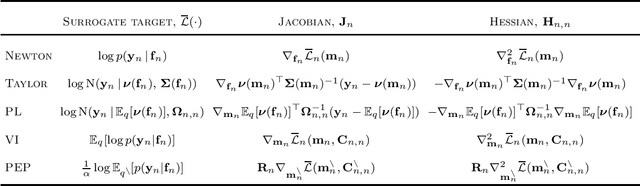
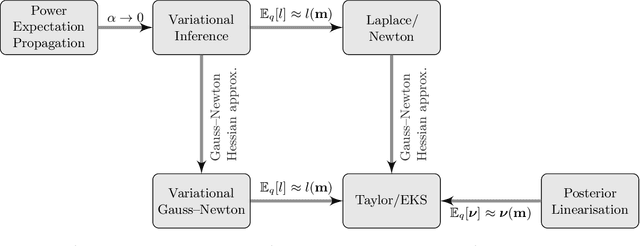
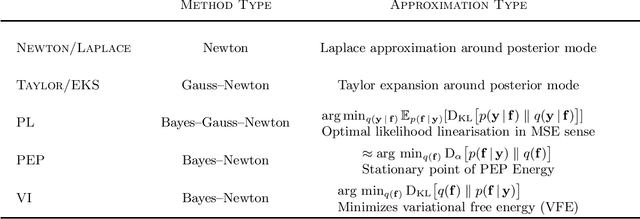

We formulate natural gradient variational inference (VI), expectation propagation (EP), and posterior linearisation (PL) as extensions of Newton's method for optimising the parameters of a Bayesian posterior distribution. This viewpoint explicitly casts inference algorithms under the framework of numerical optimisation. We show that common approximations to Newton's method from the optimisation literature, namely Gauss-Newton and quasi-Newton methods (e.g., the BFGS algorithm), are still valid under this 'Bayes-Newton' framework. This leads to a suite of novel algorithms which are guaranteed to result in positive semi-definite covariance matrices, unlike standard VI and EP. Our unifying viewpoint provides new insights into the connections between various inference schemes. All the presented methods apply to any model with a Gaussian prior and non-conjugate likelihood, which we demonstrate with (sparse) Gaussian processes and state space models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge