Barlow Twins: Self-Supervised Learning via Redundancy Reduction
Paper and Code
Mar 04, 2021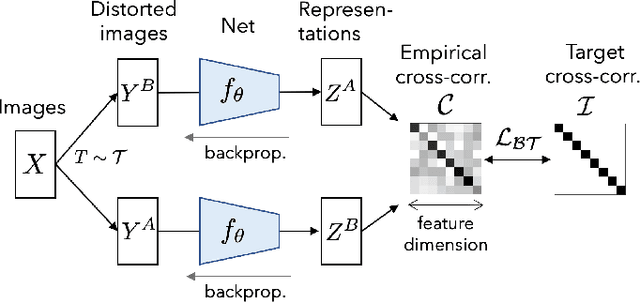
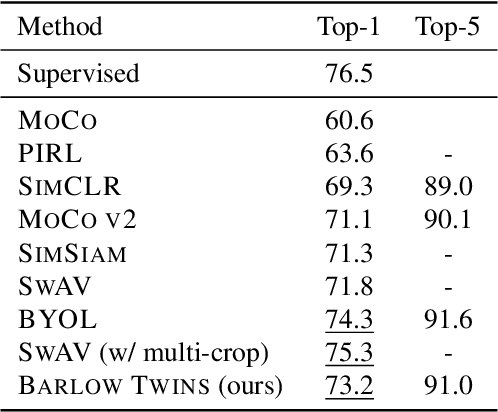
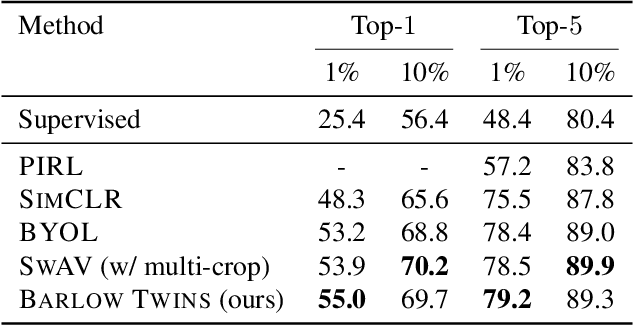
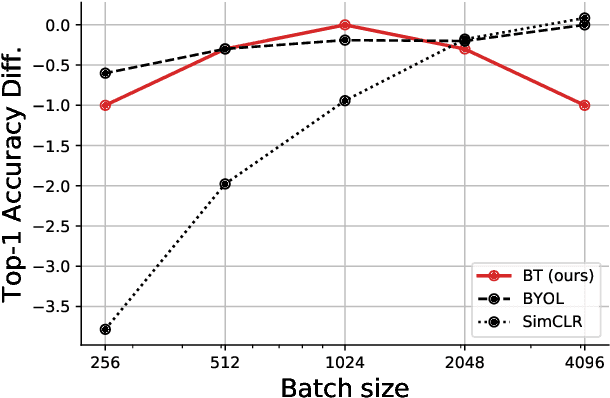
Self-supervised learning (SSL) is rapidly closing the gap with supervised methods on large computer vision benchmarks. A successful approach to SSL is to learn representations which are invariant to distortions of the input sample. However, a recurring issue with this approach is the existence of trivial constant representations. Most current methods avoid such collapsed solutions by careful implementation details. We propose an objective function that naturally avoids such collapse by measuring the cross-correlation matrix between the outputs of two identical networks fed with distorted versions of a sample, and making it as close to the identity matrix as possible. This causes the representation vectors of distorted versions of a sample to be similar, while minimizing the redundancy between the components of these vectors. The method is called Barlow Twins, owing to neuroscientist H. Barlow's redundancy-reduction principle applied to a pair of identical networks. Barlow Twins does not require large batches nor asymmetry between the network twins such as a predictor network, gradient stopping, or a moving average on the weight updates. It allows the use of very high-dimensional output vectors. Barlow Twins outperforms previous methods on ImageNet for semi-supervised classification in the low-data regime, and is on par with current state of the art for ImageNet classification with a linear classifier head, and for transfer tasks of classification and object detection.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge