Bagging in overparameterized learning: Risk characterization and risk monotonization

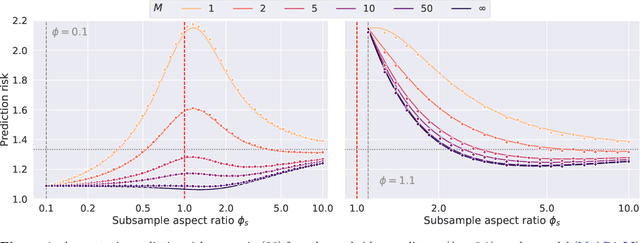
Bagging is a commonly used ensemble technique in statistics and machine learning to improve the performance of prediction procedures. In this paper, we study the prediction risk of variants of bagged predictors in the proportional asymptotics regime, in which the ratio of the number of features to the number of observations converges to a constant. Specifically, we propose a general strategy to analyze prediction risk under squared error loss of bagged predictors using classical results on simple random sampling. Specializing the strategy, we derive the exact asymptotic risk of the bagged ridge and ridgeless predictors with an arbitrary number of bags under a well-specified linear model with arbitrary feature covariance matrices and signal vectors. Furthermore, we prescribe a generic cross-validation procedure to select the optimal subsample size for bagging and discuss its utility to mitigate the non-monotonic behavior of the limiting risk in the sample size (i.e., double or multiple descents). In demonstrating the proposed procedure for bagged ridge and ridgeless predictors, we thoroughly investigate oracle properties of the optimal subsample size, and provide an in-depth comparison between different bagging variants.