Bag-of-Vector Embeddings of Dependency Graphs for Semantic Induction
Paper and Code
Sep 30, 2017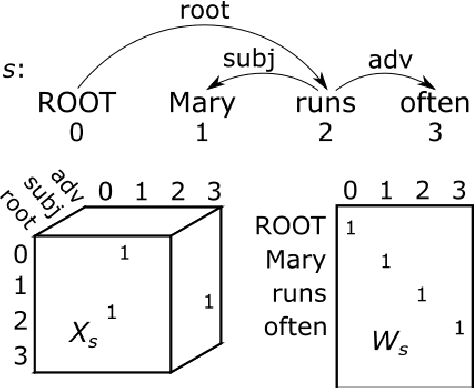
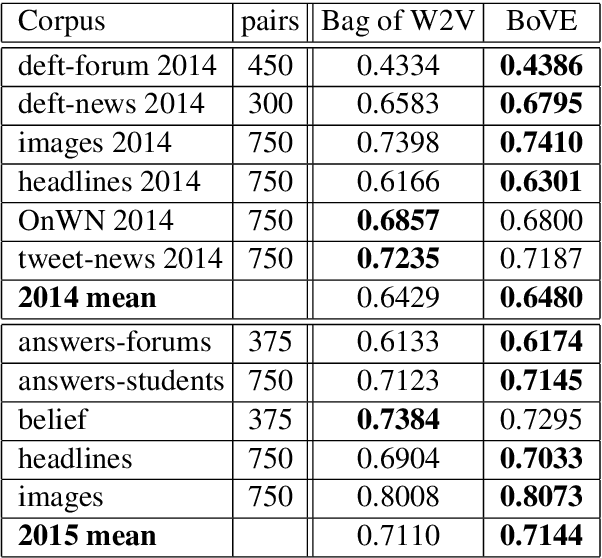
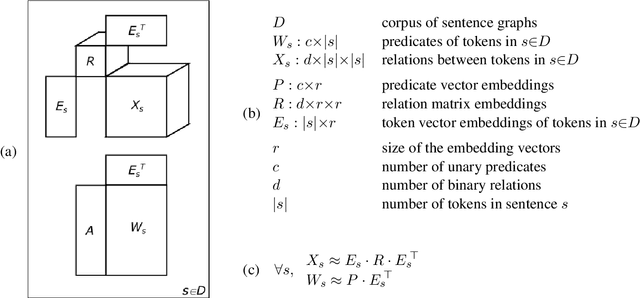
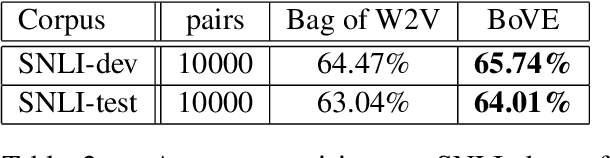
Vector-space models, from word embeddings to neural network parsers, have many advantages for NLP. But how to generalise from fixed-length word vectors to a vector space for arbitrary linguistic structures is still unclear. In this paper we propose bag-of-vector embeddings of arbitrary linguistic graphs. A bag-of-vector space is the minimal nonparametric extension of a vector space, allowing the representation to grow with the size of the graph, but not tying the representation to any specific tree or graph structure. We propose efficient training and inference algorithms based on tensor factorisation for embedding arbitrary graphs in a bag-of-vector space. We demonstrate the usefulness of this representation by training bag-of-vector embeddings of dependency graphs and evaluating them on unsupervised semantic induction for the Semantic Textual Similarity and Natural Language Inference tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge