Backprop-Q: Generalized Backpropagation for Stochastic Computation Graphs
Paper and Code
Jul 25, 2018
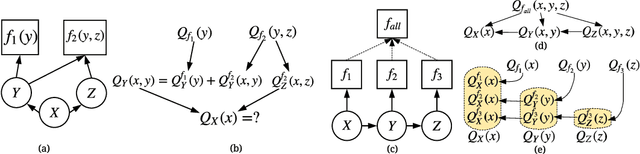
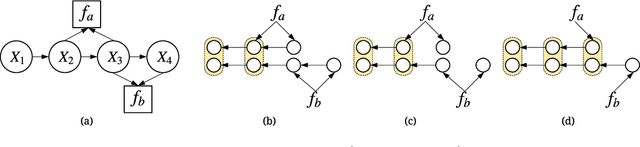
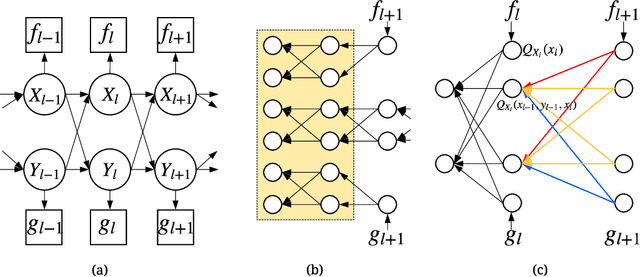
In real-world scenarios, it is appealing to learn a model carrying out stochastic operations internally, known as stochastic computation graphs (SCGs), rather than learning a deterministic mapping. However, standard backpropagation is not applicable to SCGs. We attempt to address this issue from the angle of cost propagation, with local surrogate costs, called Q-functions, constructed and learned for each stochastic node in an SCG. Then, the SCG can be trained based on these surrogate costs using standard backpropagation. We propose the entire framework as a solution to generalize backpropagation for SCGs, which resembles an actor-critic architecture but based on a graph. For broad applicability, we study a variety of SCG structures from one cost to multiple costs. We utilize recent advances in reinforcement learning (RL) and variational Bayes (VB), such as off-policy critic learning and unbiased-and-low-variance gradient estimation, and review them in the context of SCGs. The generalized backpropagation extends transported learning signals beyond gradients between stochastic nodes while preserving the benefit of backpropagating gradients through deterministic nodes. Experimental suggestions and concerns are listed to help design and test any specific model using this framework.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge