AutoFHE: Automated Adaption of CNNs for Efficient Evaluation over FHE
Paper and Code
Oct 12, 2023

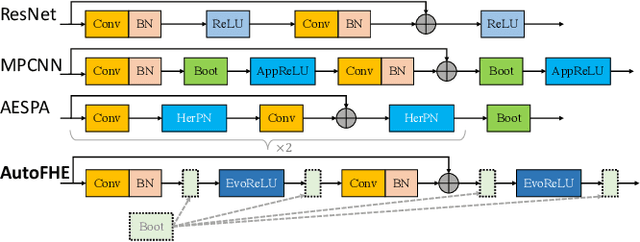
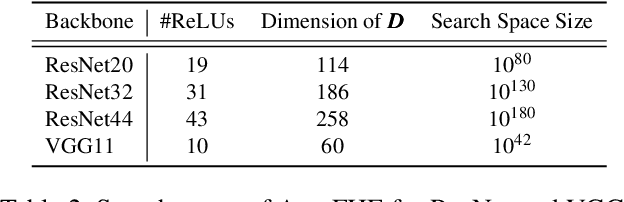
Secure inference of deep convolutional neural networks (CNNs) under RNS-CKKS involves polynomial approximation of unsupported non-linear activation functions. However, existing approaches have three main limitations: 1) Inflexibility: The polynomial approximation and associated homomorphic evaluation architecture are customized manually for each CNN architecture and do not generalize to other networks. 2) Suboptimal Approximation: Each activation function is approximated instead of the function represented by the CNN. 3) Restricted Design: Either high-degree or low-degree polynomial approximations are used. The former retains high accuracy but slows down inference due to bootstrapping operations, while the latter accelerates ciphertext inference but compromises accuracy. To address these limitations, we present AutoFHE, which automatically adapts standard CNNs for secure inference under RNS-CKKS. The key idea is to adopt layerwise mixed-degree polynomial activation functions, which are optimized jointly with the homomorphic evaluation architecture in terms of the placement of bootstrapping operations. The problem is modeled within a multi-objective optimization framework to maximize accuracy and minimize the number of bootstrapping operations. AutoFHE can be applied flexibly on any CNN architecture, and it provides diverse solutions that span the trade-off between accuracy and latency. Experimental evaluation over RNS-CKKS encrypted CIFAR datasets shows that AutoFHE accelerates secure inference by $1.32\times$ to $1.8\times$ compared to methods employing high-degree polynomials. It also improves accuracy by up to 2.56% compared to methods using low-degree polynomials. Lastly, AutoFHE accelerates inference and improves accuracy by $103\times$ and 3.46%, respectively, compared to CNNs under TFHE.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge